基本概念
機率分布是機率論的基本概念之一，用以表述隨機變數取值的機率規律。為了使用的方便，根據隨機變數所屬類型的不同，機率分布取不同的表現形式。
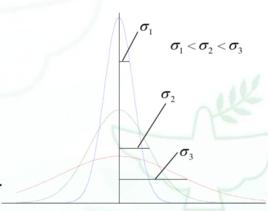
標準差也被稱為標準偏差，標準差(Standard Deviation)描述各數據偏離平均數的距離（離均差）的平均數，它是離差平方和平均後的方根，用σ表示。標準差是方差的算術平方根。標準差能反映一個數據集的離散程度，標準偏差越小，這些值偏離平均值就越少，反之亦然。標準偏差的大小可通過標準偏差與平均值的倍率關係來衡量。平均數相同的兩個數據集，標準差未必相同。
機率分布反應了該隨機變數的全貌，但在實際套用中更關係代表該機率分布的若干數字特徵量。這些特徵量主要有期望、方差、標準偏差 。
公式
機率分布標準偏差機率分布或隨機變數的標準偏差是方差的正平方根值，用符號 表示：
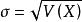機率分布標準偏差其中方差為：
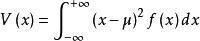機率分布標準偏差標準偏差是無窮多次測量隨機誤差平方的算術平均值的正平方根值的極限：
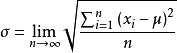機率分布標準偏差 機率分布標準偏差由於標準偏差 是無窮多次測量時的極限值，所以又稱總體標準偏差。期望和方差（或標準偏差）是表征機率分布的兩個特徵參數。理想情況下，應該以期望為被測量的測量結果，以標準偏差表示測得值的分散性。
常用機率分布及其標準偏差
二點分布和均勻分布
（1）二點分布
許多隨機事件只有兩個結果。如抽檢產品的結果合格或不合格；產品或者可靠的工作，或者失效。描述這類隨機事件變數只有兩個取值，一般取0和1。它服從的分布稱兩點分布。 其機率分布為：
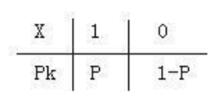機率分布標準偏差標準偏差：
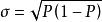機率分布標準偏差（2）均勻分布
許多隨機事件只有兩個結果。如抽檢產品的結果合格或不合格；產品或者可靠的工作，或者失效。描述這類隨機事件變數只有兩個取值，一般取0和1。它服從的分布稱兩點分布。 其機率分布為：
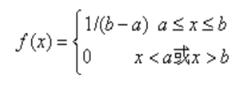機率分布標準偏差標準偏差：
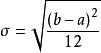機率分布標準偏差二項分布
假設有一批產品，不合格品率為P，從這批產品中隨機地抽出n件作為被檢樣品，其中不合格品數X服從的分布為二項分布。X的機率分布為：
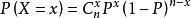機率分布標準偏差
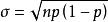機率分布標準偏差標準偏差：
泊松分布
在[0，t]時間內發生衝擊的次數X服從泊松分布，其分布機率為：
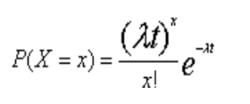機率分布標準偏差標準偏差：
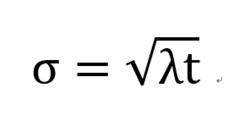機率分布標準偏差常態分配
常態分配又稱為常態分布或高斯分布。它的機率密度函式為：
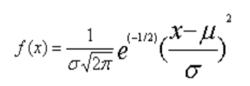機率分布標準偏差標準偏差在機率分布的套用
標準偏差σ的物理意義是：當一台確定的儀器對同一物理量進行n次重複測量時，表述該測量列隨機誤差的分散程度，σ越小。說明該儀器的精密度越好，反之精密度越差；或者，當用一台確定的儀器對一批 個（或n組）零件進行測量時，表達該組被測件隨機誤差的分散程度， σ越小，說明該批零件的工藝穩定性好，反之，工藝穩定性差。
標準偏差在實踐中的套用主要用於 ：
（1）測試儀器設備的精密度的評定；
（2）用於工藝穩定性的評定；
（3）精度檢定；
（4）用於測量爭議的間接仲裁。
