定義
分布律
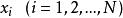累積機率分布在離散型隨機變數中，計算變數的每個可能取值 的機率，求得的結果即為分布律，滿足下式：
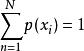累積機率分布
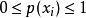累積機率分布機率密度函式
累積機率分布在連續型隨機變數中，機率密度函式（在不至於混淆時可以簡稱為密度函式）是一個描述這個隨機變數的輸出值在某個確定的取值點附近的可能性的函式。
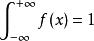累積機率分布
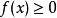累積機率分布累積機率分布
累積機率分布 累積機率分布設 是一個隨機變數， 是任意實數，函式
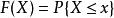累積機率分布 累積機率分布稱為 的分布函式（累積機率分布函式）
具有的性質如下：
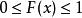累積機率分布1）
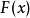累積機率分布 累積機率分布2） 是 的不減函式
計算示例
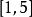累積機率分布 累積機率分布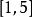 累積機率分布
累積機率分布 累積機率分布在區間上任意擲一個質點，用 表示這個質點與原點的距離，則是一個隨機變數。如果這個質點落在上任一子區間內的機率與這個區間的長度成正比，求的分布函式。
解：
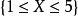累積機率分布
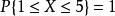累積機率分布由題意知， 是一個必然事件，則
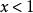累積機率分布
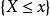累積機率分布
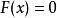累積機率分布若，則 是不可能事件，
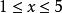累積機率分布
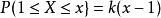累積機率分布
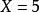累積機率分布 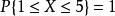累積機率分布
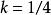累積機率分布若， 則，特別的，取，由，可得，
從而
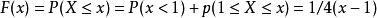累積機率分布
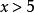累積機率分布
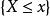累積機率分布
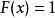累積機率分布若，則 是必然事件，
綜上所述：
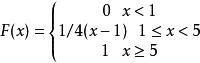累積機率分布圖像的累積機率分布
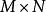累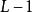積機率分布
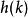累積機率分布
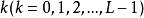累積機率分布
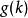累積機率分布
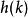累積機率分布 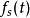累積機率分布
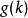累積機率分布
累積機率分布
累積機率分布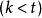
累積機率分布設 像素大小圖像的最大灰度級為，圖像的灰度直方圖為具有灰度級的像素個數。灰度級分布機率的值是除以圖像總的像素個數。圖像的累積機率分布為的前項之和，表示為：
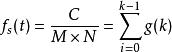累積機率分布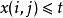
累積機率分布
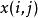累積機率分布
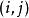累積機率分布
累積機率分布
累積機率分布其中，—— 的個數，——圖像在像素處的像素值，——圖像灰度級。
