機構自由度
正文
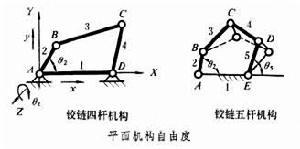
使機構具有確定運動時所必須給定的獨立運動數目。圖為平面鉸鏈四桿機構,當構件2按給定的角位移規律θ2＝θ2(t)運動時,其餘各構件的運動就隨之確定，因而該機構的自由度數為1。構件2是機構中接受外界獨立運動的構件，稱為機構的主動件，其餘構件稱為從動件。欲使機構具有確定運動，應使機構的主動件數等於其自由度數。若機構的主動件數少於機構自由度數,如圖的平面鉸鏈五桿機構,只給定主動件 2一個獨立運動參數，即構件的角位移規律θ2＝θ2(t)時,則其餘構件3、4、5的運動並不能確定。若機構的主動件數多於自由度數，則可能使其中驅動功率較小的主動件被迫變為從動件，或使機構卡住不動，甚至遭到破壞。但是，對於平面鉸鏈五桿機構，再給定構件5的角位移規律θ5＝θ5(t)時，即同時給定兩個獨立的運動參數，則此五桿機構的運動完全確定。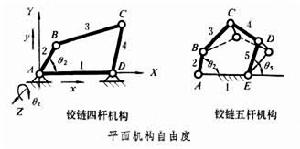
機構自由度F =3n-2P1-Ph (1)
式中n為一個平面機構中活動構件數(機架作為參考坐標系不計算在內)，每個活動構件有3個自由度，即圖中沿X、Y 軸的獨立移動和繞Z軸的獨立轉動θz；P1為低副數,每個低副引進2個約束,即限制2個自由度,其中轉動副(如圖中A)限制x、y兩個移動，移動副限制1個轉動和另1個移動；Ph為高副數，每個高副只引進1個約束，即限制1個自由度。套用平面機構自由度的計算公式時需要注意複合鉸鏈，局部自由度和虛約束等幾種情況。當幾個轉動副的軸線重合時稱為複合鉸鏈，在計算轉動副數時不能遺漏。凸輪機構中從動件如帶有滾子，滾子的自轉運動即為局部自由度，在計算機構的自由度時應將局部自由度除去不計。機構中引進局部自由度的主要目的是為了減小磨損。虛約束是不起約束作用的約束，當一根軸用兩個軸承而形成兩個軸線並行的轉動副時，其中一個即為虛約束。機構中引進虛約束僅僅是為了提高零件的剛度或渡過機構的死點，但對製造和安裝的要求有所提高；否則虛約束就成為實約束，從而使機構產生卡住現象。
計算空間機構的自由度時, 所用的公式類似式 (1)，但每個活動構件有 6個自由度；x、y、z、θx、θy和θz。空間運動副可按其相對約束數分為5類，例如球面副有3個相對約束，即x、y、z，稱為Ⅲ類運動副；轉動副有5 個相對約束，即x、y、z、θx、θy，稱為Ⅴ類運動副；其餘類推。機構中每個構件受到的或每個運動副具有的相同的約束稱為公共約束，如圖所示的平面鉸鏈四桿機構中,其所有構件只能在X、Y 平面內運動，這就使這一平面機構的所有構件的運動受到相同的公共約束,即均不能沿Z 軸移動和繞X 及Y 軸轉動,亦即該機構的所有構件共同受到3個公共約束。以
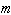表示機構的公共約束數，則機構中每個活動構件的自由度數和每個運動副的有效約束都要減少個。這樣，空間機構自由度的計算公式為 
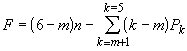(2)
F＝6n-5P5-4P4-3P3-2P2-P1(3)
平面機構以受到Z、θx和θy三個公共約束，m＝3，所以F＝3n-2P5-P4 (4)
式中P5和P4相應為式(1)中的P1和Ph。m的概念是在1936年由蘇聯學者提出來的；關於m的具體求法是1952年中國學者最先提出來的"脫離機架法"。這個公式僅適用於求單環機構的自由度。對於多環機構的自由度，中國學者在1979年提出一種比較簡單的方法，即先將各環分別按單環計算，最后綜合考慮。
