介紹
剛度是使物體產生單位變形所需的外力值。剛度與物體的材料性質、幾何形狀、邊界支持情況以及外力作用形式有關。材料的彈性模量和剪下模量(見材料的力學性能)越大,則剛度越大。細桿和薄板在受側向外力作用時剛度很小,但細桿和薄板如果組合得當,邊界支持合理,使桿只承受軸向力,板只承受平面內的力,則它們也能具有較大的剛度。
在自然界,動物和植物都需要有足夠的剛度以維持其外形。在工程上,有些機械、橋樑、建築物、飛行器和艦船就因為結構剛度不夠而出現失穩,或在流場中發生顫振等災難性事故。因此在設計中,必須按規範要求確保結構有足夠的剛度。但對剛度的要求不是絕對的,例如,彈簧秤中彈簧的剛度就取決於被稱物體的重量範圍,而纜繩則要求在保證足夠強度的基礎上適當減小剛度。
研究剛度的重要意義還在於,通過分析物體各部分的剛度,可以確定物體內部的應力和應變分布,這也是固體力學的基本研究方法之一。
結構的靜剛度與動剛度
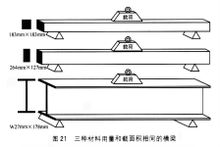 剛度
剛度靜載荷下抵抗變形的能力稱為靜剛度。動載荷下抵抗變形的能力稱為動剛度,即引起單位振幅所需的動態力。如果幹擾力變化很慢(即干擾力的頻率遠小於結構的固有頻率),動剛度與靜剛度基本相同。干擾力變化極快(即干擾力的頻率遠大於結構的固有頻率時),結構變形比較小,即動剛度比較大。當干擾力的頻率與結構的固有頻率相近時,有共振現象,此時動剛度最小,即最易變形,其動變形可達靜載變形的幾倍乃至十幾倍。
構件變形常影響構件的工作,例如齒輪軸的過度變形會影響齒輪嚙合狀況,工具機變形過大會降低加工精度等。影響剛度的因素是材料的彈性模量和結構形式,改變結構形式對剛度有顯著影響。剛度計算是振動理論和結構穩定性分析的基礎。在質量不變的情況下,剛度大則固有頻率高。靜不定結構的應力分布與各部分的剛度比例有關。在斷裂力學分析中,含裂紋構件的應力強度因子可根據柔度求得。
基本公式
k=P/δ
其中 k表示剛度, P表示施力,δ表示變形量(變形後的長度減去原長或原長減去變形後的長度)。在國際單位制中,剛度的單位為牛/米。一般套用於胡克定律作系統的振動分析。
位移
計算剛度的理論分為小位移理論和大位移理論。大位移理論根據結構受力後的變形位置建立平衡方程,得到的結果精確,但計算比較複雜。小位移理論在建立平衡方程時暫時先假定結構是不變形的,由此從外載荷求得結構內力以後,再考慮變形計算問題。大部分機械設計都採用小位移理論。例如,在梁的彎曲變形計算中,因為實際變形很小,一般忽略曲率式中的撓度的一階導數,而用撓度的二階導數近似表達梁軸線的曲率。這樣做的目的是將微分方程線性化,以大大簡化求解過程;而當有幾個載荷同時作用時,可分別計算每個載荷引起的彎曲變形後再疊加。
彈性模量
一般來說,剛度和彈性模量是不一樣的。彈性模量是物質組分的性質;而剛度是結構的性質。也就是說,彈性模量是物質微觀的性質,而剛度是物質巨觀的性質。
材料力學中,彈性模量與相應截面幾何性質的乘積表示為各類剛度,如GI為扭轉剛度,EI為彎曲剛度,EA為拉壓剛度。
工程力學、工程結構、建築材料
| ▪工程力學 | ▪固體力學 | ▪材料力學 | ▪剛體 | ▪彈性體 |
| ▪約束 | ▪力系 | ▪力矩 | ▪力偶 | ▪摩擦 |
| ▪功 | ▪功率 | ▪動能 | ▪勢能 | ▪衝量 |
| ▪動量 | ▪變形 | ▪動量矩 | ▪位移 | ▪撓度 |
| ▪拉伸 | ▪壓縮 | ▪剪下 | ▪彎曲 | ▪扭轉 |
| ▪內力 | ▪應力 | ▪主應力 | ▪莫爾圓 | ▪應變 |
| ▪強度 | ▪剛度 | ▪勁度 | ▪硬度 | ▪彈性模量 |
| ▪剪下模量 | ▪泊松比 | ▪衝擊韌度 | ▪截面模量 | ▪截面面積矩 |
| ▪轉動慣量 | ▪截面迴轉半徑 | ▪慣性半徑 | ▪應力集中 | ▪接觸應力 |
| | | | | |
其他科技名詞
套用
在工程套用中,結構的剛度是十分重要的,因此在選擇材料時彈性模量是一個重要指標。當有不可預測的大撓度時,高的彈性模量是十分必要的。當結構需要有好的柔韌性時,就要求彈性模量不要太高。

