正文
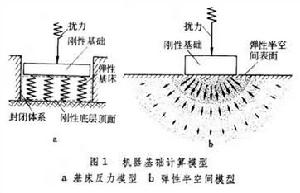
基床反力模型 假定剛性基礎位於有彈性而無慣性的地基上，地基是由許多獨立的彈簧組成並坐落在一個假想的剛性底層上（圖1a），振動限於該範圍內發生。
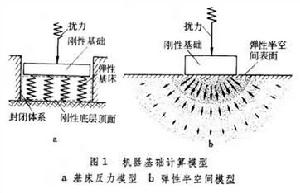機器基礎計算模型P＝czz (1)
式中cz為地基抗壓剛度係數，是不隨頻率改變的常數。
總的動反力R＝(czF)z＝Kzz式中Kz為地基抗壓剛度；F為基底面積。
基礎的運動方程為
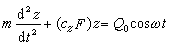(2)
式 (2)和理想的質量──彈簧體系的模式完全一樣。這種模型未能就動力參數Cz建立起理論公式。為取得Cz：①要靠查表取得cz的經驗值，其餘抗剪、抗彎、抗扭剛度係數Cx、C嗞、Cψ通過與Cz的經驗比值求得；②要靠現場試驗，過去是採用高低壓模自由振動試驗，現在出現了一些強迫振動試驗的方法。但是，在任何一種試驗方法中，Cz都是在不隨頻率改變的假定下獲得的。據此算出的共振曲線與實測共振曲線不盡相符。
四個簡單振型的剛度，可按下式求得：
垂直振動時，地基抗壓剛度Kz＝czF
水平振動時，地基抗剪剛度Kx＝cxF
搖擺振動時，地基抗彎剛度K嗞＝c嗞I1
扭轉振動時，地基抗扭剛度Kψ＝cψI1式中I1為對於通過基底形心的水平軸的面積慣性矩；I1為對於通過基底形心的豎直軸的面積慣性矩（亦稱極慣性矩）。
彈性半空間模型 視剛性基礎位於彈性半空間表面上，彈性半空間是一個各向同性的、均質的、上面有界、以下及左右前後伸至無窮的彈性體，這種模型所涉及的土的範圍（不論廣度或深度）可擴展至無窮（圖1b）。按此模型，以垂直振動為例，基礎的動位移與波動力（與動反力相反，是基底傳予地基的動力，一般不等於擾力）間具有以下關係：
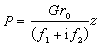(3)
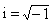;f1、f1為位移函式,它們與基礎尺寸、地基土的性質及擾動頻率有關。 根據式(3)導出垂直振動的動反力公式為
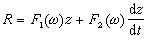(4)
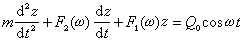(5)
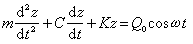對比，可見置於半空間上的基礎的模式與理想集總體系模式外形相似而實質不同，即 F1(ω)、F1（ω）不再是常數而是頻率的函式，故式(5)可稱為等效集總體系的模式，而其相應的F1(ω)、F1(ω)可分別稱為等效阻尼、等效剛度。 這樣，彈性半空間模型可以轉化為等效集總體系模型。這一事實說明：從實用出發,基礎-地基體系可以看成是質量-彈簧-阻尼器體系，然而它卻不是一個理想集總體系。這個發現推動了半空間理論實用解的發展。現今的比擬法和方程對等法都是在此基礎上產生的。 半空間模型已導出參數F1(ω)、F1(ω)的公式可供直接運用。此外,F1(ω)、F1(ω)或f1、f1還可通過現場強迫振動試驗測得。例如藉助於垂直強迫振動利用下式
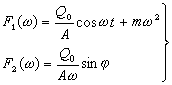(6)
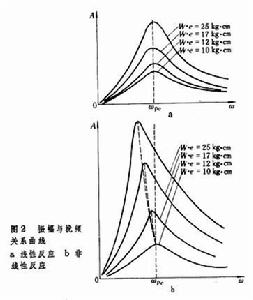
非線性反應 在擾頻率不變的條件下,擾力增大(以頻變擾力為例則意味著偏心塊重量W＝meɡ與偏心距e的乘積的增大）時，並不保證振幅成正比地（即線性地，如圖2a所示）增大，此種動力反應稱非線性反應。非線性反應不僅表現為圖2b中在任一指定頻率時的縱距不是按比例地增大,而且還表現為峰點頻率(ωpe)也隨W、e的乘積的變化而變化。機器基礎非線性反應之所以出現是因為擾力越大，剪應力和剪應變也越大,結果阻尼比增大,剪下模量減小從而使剛度減小。更確切些說，動力反應的非線性來源於土的應力應變特性的非線性。土的非線性說明彈性半空間理論關於彈性（線彈性）的假定與土的實際性狀有出入，因此欲提高預計機器基礎動力反應的可靠性，需要計入土的非線性應力應變特性。
機器基礎計算模型