名詞釋義
代數名詞
線上性代數中，一個內積空間的 正交基（orthogonal basis）是元素兩兩正交的基。稱基中的元素為 基向量。假若，一個正交基的基向量的模長都是單位長度1，則稱這正交基為 標準正交基（Orthonormal basis）。
無論在有限維還是無限維空間中，正交基的概念都是很重要的。在無限維希爾伯特空間中，正交基不再是 哈默爾基，也即是說不是每個元素都可以寫成有限個基中元素的線性組合。因此在無限維空間中，正交基應該被更嚴格地定義為由線性無關而且兩兩正交的元素組成、張成的空間是原空間的一個稠密子空間（而不是整個空間）的集合。
注意，在沒有定義內積的空間中，“正交基”一詞是沒有意義的。因此，一個巴拿赫空間有正交基，若且唯若它是一個希爾伯特空間。
簡單範例
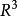標準正交基(1). a=(1/4,-1/4,1);b=(2,-2,-1);c=(1,1,0)是的一組正交基；
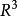標準正交基(2). α=(1,0,0);β=(0,1,0);γ=(0,0,1)是的一組標準正交基。
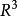標準正交基(3)在歐幾里德空間中，集合：{ e=(1,0,0), e=(0,1,0), e=(0,0,1)}組成一個標準正交基。
(4)由 f( x) = exp（2π inx）定義的集合：
{ f: n∈ Z}組成在復勒貝格空間L（[0,1]）上的一個標準正交基。
n維歐式空間V中，n個向量的正交向量組稱為V的正交基，由單位向量組成的正交基稱為標準正交基。由單位向量構成的並且相互正交的基稱為標準正交基。正交，意為兩向量的內積等於零
注: ① 由正交基的每個向量單位化,可得到一組標準正交基。 ② n維歐氏空間V中的一組基為標準正交基。
基本性質
B是 H上的一個正交基，那么 H中的每個元素 x都可以表示成：
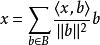標準正交基當 B是標準正交基時，就是：
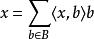標準正交基x的模長表示為：
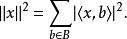標準正交基即使 B不是可數的，上面和式里的非零項也只會有可數多個，所以這個表達式仍然是有效的。上式被稱作 x的 傅立葉展開，詳見傅立葉級數。
若 B是 H上的一個標準正交基，那么 H“同構”於序列空間 l（ B）。因為存在以下 H-> l（ B）的雙射Φ，使得對於所有 H中的 x和 y有：
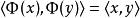標準正交基存在性
運用佐恩引理和格拉姆-施密特正交化方法，可以證明每個希爾伯特空間都有基，並且有正交基。同一個空間的正交基的基數必然是相同的。當一個希爾伯特空間有可數個元素組成的正交基，就說這個空間是可分的。
哈默爾基
有前面的定義可以知道，在無窮維空間的情況下，正交基不再是一般線性代數的定義下的基。為了區分，把一般線性代數的定義下的基稱為哈默爾基。
在內積空間的實際套用中，哈默爾基甚少出現，因此提到“基”的概念時，一般指的是正交基。
