定義
向量
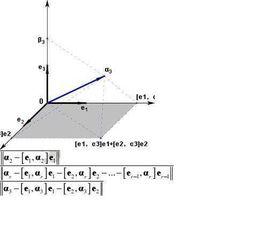
在數學中,向量(也稱為歐幾里得向量、幾何向量、矢量),指既有大小又有方向的量。它可以形象化地表示為帶箭頭的線段。
箭頭所指:代表向量的方向;
線段長度:代表向量的大小。
與向量對應的只有大小,沒有方向的量叫做數量(物理學中稱標量)。
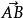 正交向量
正交向量向量的記法:印刷體記作粗體的字母(如 a、 b、 u、 v),或者 (即從起點A出發指向終點B的向量)。在空間直角坐標系中,也能把向量以數對形式表示,例如Oxy平面中用(2,3)表示向量。
在物理學和 工程學 中,幾何向量更常被稱為矢量。許多物理量都是矢量,比如一個物體的位移,球撞向牆而對其施加的力等等。與之相對的是標量,即只有大小而沒有方向的量。一些與向量有關的定義亦與物理概念有密切的聯繫,例如向量勢對應於物理中的勢能。
歐幾里得空間
 正交向量
正交向量 正交向量
正交向量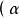 正交向量
正交向量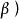 正交向量
正交向量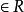 正交向量
正交向量設 是實數域R上的有限維線性空間,在 上定義有被稱為內積的滿足一下四條公理的實函式 , :
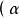 正交向量
正交向量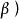 正交向量
正交向量 正交向量
正交向量 正交向量
正交向量(1)對稱性: , =( , );
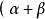 正交向量
正交向量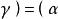 正交向量
正交向量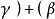 正交向量
正交向量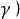 正交向量
正交向量(2)關於向量加法的線性性質: , , , ;
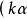 正交向量
正交向量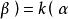 正交向量
正交向量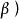 正交向量
正交向量(3)關於標量乘法的線性性質: , , ;
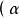 正交向量
正交向量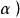 正交向量
正交向量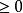 正交向量
正交向量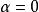 正交向量
正交向量(4)正定性: , ,而且等號成立若且唯若 。
 正交向量
正交向量 正交向量
正交向量 正交向量
正交向量 正交向量
正交向量 正交向量
正交向量這裡 , , 是 的任意向量,k是任意實數。則稱 為 歐幾里得空間(Euclidean space),簡稱 歐式空間。
 正交向量
正交向量 正交向量
正交向量 正交向量
正交向量 正交向量
正交向量 正交向量
正交向量 正交向量
正交向量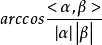 正交向量
正交向量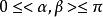 正交向量
正交向量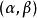 正交向量
正交向量歐幾里得空間中兩個非零向量 , 的夾角< , >定義為< , >= ,因而 。所以向量的內積為 。
正交
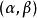 正交向量
正交向量 正交向量
正交向量 正交向量
正交向量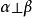 正交向量
正交向量如果 =0,則稱向量 與 正交(orthogonal),也稱 垂直(perpendicular),記為。
性質
性質1
對兩個向量x和y有內積性質(x,ky)=k(x,y)。
性質2
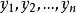 正交向量
正交向量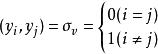 正交向量
正交向量設為n單位正交向量組,則有。
定理
定理1
 正交向量
正交向量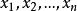 正交向量
正交向量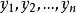 正交向量
正交向量對於歐式空間的任一基都可以找到一個標準正交基。即 任一非零歐式空間都有正交基和標準正交基。
定理2
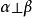 正交向量
正交向量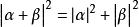 正交向量
正交向量(勾股定理)如果,則有。