方法簡介
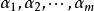 施密特正交化
施密特正交化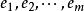 施密特正交化
施密特正交化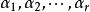 施密特正交化
施密特正交化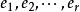 施密特正交化
施密特正交化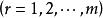 施密特正交化
施密特正交化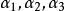 施密特正交化
施密特正交化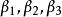 施密特正交化
施密特正交化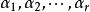 施密特正交化
施密特正交化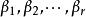 施密特正交化
施密特正交化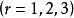 施密特正交化
施密特正交化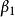 施密特正交化
施密特正交化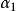 施密特正交化
施密特正交化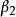 施密特正交化
施密特正交化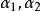 施密特正交化
施密特正交化線性無關向量組未必是正交向量組,但正交向量組又是重要的,因此現在就有一個問題:能否從一個線性無關向量組 出發,構造出一個標準正交向量組 ,並且使向量組 與向量組 等價 呢?回答是肯定的,通過施密特正交化方法就可以實現。下面就來介紹這個方法,由於把一個正交向量組中每個向量經過單位化,就得到一個標準正交向量組,所以,上述問題的關鍵是如何由一個線性無關向量組來構造出一個正交向量組,我們以3個向量組成的線性無關組為例來說明這個方法。設向量組 線性無關,我們先來構造正交向量組 ,並且使 與向量組 等價 。按所要求的條件, 是 的線性組合, 是 的線性組合,為方便起見,不妨設
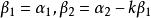 施密特正交化
施密特正交化 施密特正交化
施密特正交化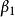 施密特正交化
施密特正交化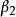 施密特正交化
施密特正交化其中,數值 的選取應滿足 與 垂直,即
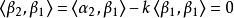 施密特正交化
施密特正交化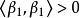 施密特正交化
施密特正交化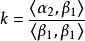 施密特正交化
施密特正交化注意到 ,於是得 ,從而得
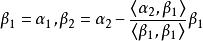 施密特正交化
施密特正交化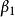 施密特正交化
施密特正交化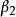 施密特正交化
施密特正交化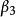 施密特正交化
施密特正交化對於上面已經構造的向量 與 ,再來構造向量 ,為滿足要求,可令
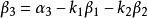 施密特正交化
施密特正交化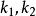 施密特正交化
施密特正交化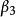 施密特正交化
施密特正交化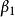 施密特正交化
施密特正交化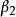 施密特正交化
施密特正交化其中, 的選取應滿足 分別於向量 與 垂直,即
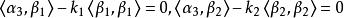 施密特正交化
施密特正交化由此解得
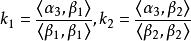 施密特正交化
施密特正交化於是得
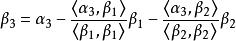 施密特正交化
施密特正交化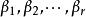 施密特正交化
施密特正交化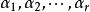 施密特正交化
施密特正交化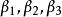 施密特正交化
施密特正交化容易驗證,向量組 是與 等價的正交向量,若再將 單位化,即令
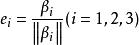 施密特正交化
施密特正交化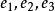 施密特正交化
施密特正交化則 就是滿足要求的標準正交向量組。
定理
一般地,用數學歸納法可以證明:
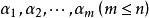 施密特正交化
施密特正交化 施密特正交化
施密特正交化設 是 中的一個線性無關向量組,若令
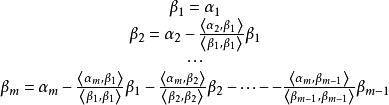 施密特正交化
施密特正交化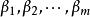 施密特正交化
施密特正交化則 就是一個 正交向量組,若再令
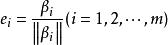 施密特正交化
施密特正交化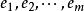 施密特正交化
施密特正交化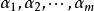 施密特正交化
施密特正交化就得到一個標準正交向量組 ,且該向量組與等價。
上述所說明的利用線性無關向量組,構造出一個標準正交向量組的方法,就是施密特正交化方法。

