核集團模型
正文
一種原子核結構模型。這種模型認為核核心子結合成若干“集團”,而原子核則通過這些集團之間的相互作用結合在一起。核子以集團的形式出現於核內,使集團內部的自由度可以近似地凍結,並引入集團整體的定域坐標(例如集團之間的相對坐標),從而使計算簡化。這種近似方法和著重考慮單粒子運動的核殼層模型各自強調了核結構的某一個側面,因而可以說這兩種模型只是描寫了兩個極端情況。在滿殼附近單粒子效應比較明顯;而在另外一些情況下集團效應比較明顯。實驗表明,輕核中有比較明顯的集團現象,重核的表面也存在集團現象。因而,集團模型通常被用來研究輕核的性質,處理核少體問題,並取得了一定的成功。最主要的理論方法有共振群方法和生成坐標方法。
共振群方法 (RGM) 共振群方法是J.A.惠勒於1937年首先提出的。在這個方法中,原子核的嘗試波函式由集團內部波函式和相對運動波函式組成。從薛丁格方程出發,對集團的內部坐標積分,就可得到相對運動波函式g(R)所滿足的積分-微分方程。
共振群方法的優點在於它能直接得到物理意義明確而且十分有用的相對運動波函式,因而被廣泛用來研究輕核的結構、核的散射及反應問題,並且取得了較好的結果。下圖給出了3He+α散射的微分截面,可以看到理論計算同實驗結果符合是令人滿意的。但是由於反對稱化的要求,使積分核的計算相當繁複,以致於對較重的原子核系統的計算帶來幾乎難以克服的困難。
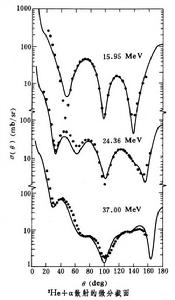 核集團模型
核集團模型通過對生成坐標中權函式的一個積分變換可以得到GCM和RGM的關係式
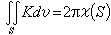 ,
,
