核少體問題
正文
原子核物理學中的重要問題之一。它研究由少數核子組成的體系的結構特性和反應規律。涉及到的核子數少,研究便比較深入,可以期望以此揭示核子間的相互作用的基本規律,並為探討更複雜的核結構和反應問題提供必要的基礎;研究中發展起來並經過檢驗的實驗和理論方法,有可能推廣到核多體問題中去。此外,在天體物理和核能套用中,核少體問題也是重要的,因為釋放大量核能的熱核聚變反應正是少體核之間的反應。例如提供太陽能源的由4個氫核逐步合成氦核的p-p鏈反應。又如作為核聚變反應堆的工作基礎的反應:
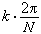
核少體問題中,最早被人們注意而且討論得最多的,是關於氘核束縛態和二核子間散射的二體問題。通過對這些現象的研究,現在已經相當詳細地推知了二核子間相互作用的唯象勢(見核力)。
20世紀60年代以來,核三體問題的實驗和理論研究已有了長足的進步,目前它還是引起許多工作者注意的課題。L.D.法捷耶夫為三體問題建立了嚴格的積分方程──法捷耶夫方程。這個方程可以推廣到核子數A≥4的系統中去:研究A個核子體系時,廣義法捷耶夫方程的積分核和非齊次部分可以用二體、………、(A-1)體問題的解表示出來,所以原則上可以用法捷耶夫形式逐步嚴格求解核少體問題。不過,隨著A的增大,公式很快複雜化,計算繁複到無法進行,所以還很少有人嘗試用廣義的法捷耶夫方程求解四體以上問題。
近年來實際處理核少體問題時套用較多的是在變分原理基礎上發展起來的核集團模型方法──共振群方法。下面簡單介紹這個方法的大意。
描寫A個核子系統穩態的波函式ψ=ψ(r1,r2,…,rA)滿足薛丁格方程
Hψ=Eψ, (1)
式中哈密頓算符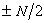 , (2)
, (2)
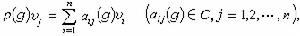 , (3)
, (3)
 表示對所有連續變數的積分和所有離散變數的求和。嘗試函式ψ 可以選取為某一完全函式系{嗞i}的線性疊加
表示對所有連續變數的積分和所有離散變數的求和。嘗試函式ψ 可以選取為某一完全函式系{嗞i}的線性疊加 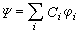 , (4)
, (4)
嗞i(r1,…,rA)─→嗞i(α1,…,αn;r1,…,rA)。
在集團模型計算中,通常假設A個核子在一振子勢中運動,並略去質子與中子質量間的差別,把mk都寫作m,這時哈密頓量H可寫成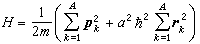 , (5)
, (5)
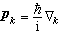 是第k個核子的動量算符,
是第k個核子的動量算符,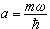 是圓頻率為ω的振子勢的寬度參量。將A個核子分成l個集團,其中第k個集團包含nk個核子,
是圓頻率為ω的振子勢的寬度參量。將A個核子分成l個集團,其中第k個集團包含nk個核子,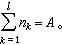 {n1,n2,…,nl}稱為核的集團表示。引進這些集團的質心坐標
{n1,n2,…,nl}稱為核的集團表示。引進這些集團的質心坐標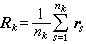 和質心動量
和質心動量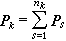 ,式(5)中H 量可改寫為
,式(5)中H 量可改寫為 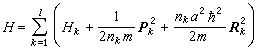 ,
,
參考書目
T.Lauritsen and F.Ajzenberg-Selove,Nucl.phys.A,Vol.78,p.1,1966.
L.D.Faddeev, Three Body Problem, North-Holland,Amsterdam,1970.
K.Wildermuth and Y.C.Tang,A Unified Theory ofthe Nucleus,Academic Press, New York, 1977.