衛星大地測量學
正文
研究利用人造地球衛星進行地麵點定位以及測定地球形狀、大小和地球重力場的理論和方法的學科。作用 1957年人造地球衛星的出現,給大地測量帶來了巨大變革。1958年僅根據對蘇聯“人造地球衛星”2號幾個星期目視觀測資料,就推得較準確的地球扁率為1:298.24。1959年又按“先鋒”1號衛星的觀測數據,進一步推知地球的南、北半球不對稱,大地水準面在北極處隆起約10米,南極處下陷約20多米。這兩項成就說明了衛星大地測量學可以解決常規大地測量長期難以解決的問題。
60年代,按人造地球衛星的觀測數據求出了較精確的地球引力場模型和解析度達幾百公里的大地水準面起伏。70年代子午衛星都卜勒觀測技術的廣泛套用,測定了遍及全球的地面站的地心坐標。雷射對衛星測距達到厘米級的精度,並製成了流動式雷射測距儀,可以測定地面站精確位置、極移和地球自轉的短周期變化。利用“吉奧斯”3號衛星的星載雷達測高技術,首次成功地測定了海洋表面形狀,從而可以比較精確地推求全球大地水準面。
大地測量衛星 用於大地測量的衛星有些裝有各種儀器,如閃光燈、無線電發射機、雷達測高儀、重力梯度儀和衛星跟蹤衛星的測量系統等。另一些氣球衛星或裝有雷射反射鏡的衛星,是以反射陽光或反射來自地面的雷射束供觀測者對衛星進行觀測。已知的主要大地測量衛星如表。 衛星大地測量方法 衛星大地測量在原理上分為幾何法和動力法。將衛星作為高空觀測目標,由幾個地面站同步觀測,即可按三維三角測量法計算這些站的相對位置,實現遠距離的大地聯測。這種方法不涉及衛星的軌道運動,稱為衛星大地測量幾何法。如果利用衛星距地球較近的特點,將它作為地球引力場的敏感器進行軌道攝動觀測,就可推求地球形狀和引力場參數,同時可以精確計算衛星軌道和確定地面站的坐標。由於衛星沿著以地球質心為其焦點之一的橢圓軌道運行,所以這樣測定的地面站坐標是相對於地球質心的絕對位置。這種測量方法稱為衛星大地測量動力法。
衛星大地測量幾何法 原理如圖1。由地面上A、B兩站同步觀測至衛星S1的方向AS1和BS1,在另一時刻同步觀測至衛星S2的方向AS2和BS2,則由平面ABS1和ABS2的交線可確定A、B間的弦方向AB。在其他測站間重複上述觀測過程,即可得出由各測站間的弦方向所構成的空間三角網。如果再由地面測量或由地面至衛星的雷射測距,提供出三角網的長度因子(即在空間三角網解算中決定長度的要素),就可以推算出各測站點的相對坐標。
60年代,很多國家曾用幾何法建立空間三角網和地面三角網的洲際聯測。其中規模較大的是美國國家大地測量局主持的世界人造衛星三角網聯測。它包括分布在全球的45個測站,網點間的距離為4000~4500公里,網的長度因子由長為1200~3500公里的 7條地面基線提供。這些基線分別位於北美、歐洲、非洲和澳大利亞,用電磁波測距儀測量。整個網經過平差後,點的坐標的中誤差平均為±4.7米,網的平均長度相對誤差為 ±5×10-7。
衛星大地測量動力法 根據衛星在軌道上受攝動力的運動規律,利用地面站對衛星的觀測數據,可以同時計算衛星軌道根數、地球引力場參數和地面觀測站地心坐標。
地球引力、大氣阻力、日月引力、太陽光壓、地球潮汐(海潮、固體潮和大氣潮)等對衛星軌道都有影響,研究和測定衛星軌道在這些影響之下的變化,是衛星大地測量動力法的基礎。 如果地球是一個質量均勻分布的圓球,則地球對衛星的引力相當於假定地球質量集中於其中心時對衛星的引力。按克卜勒(J.Kepler)的行星運動定律,這時衛星的軌道是一個不變化的橢圓,地球位於其焦點之一。這個軌道橢圓由6個軌道根數i、Ω、ɑ、e、ω和T來確定(圖2)。i為軌道傾角,即軌道平面同赤道平面的夾角;Ω為升交點的赤經,即衛星軌道投影到天球上,同天球赤道相交的兩點中,衛星由南向北通過赤道的那一點的赤經;ɑ和e分別為軌道橢圓的長半徑和偏心率;ω為近地點角距,即近地點到升交點的角距;T為衛星通過近地點的時刻;v為真近點角,即衛星到近地點的角距,有的文獻以它代替T作為軌道根數。這6個軌道根數中ɑ和e可確定軌道橢圓的形狀和大小,i和Ω確定軌道面相對於地球的空間位置,ω說明軌道橢圓在空間的定向,T是推算衛星位置的時間起點。
實際上,地球的質量分布極不均勻,它的形狀雖近似於一個鏇轉橢球,但很不規則,因而地球引力場非常複雜。衛星在繞地球運行中,除受到地球不規則引力場的攝動外,還受到大氣阻力、日月引力、太陽光壓和地球潮汐等攝動力的作用,因而衛星軌道不是一個不變的橢圓,其形狀、大小和在空間的位置都在不斷地變化。任一瞬間同這個軌道相密切的橢圓稱密切橢圓。在攝動情況下,認為衛星軌道是隨時間變化的瞬時橢圓。
衛星的運動方程是一個非常複雜的微分方程,可按級數展開法求解。此法把某一時刻t0的密切橢圓軌道作為固定的參考軌道,而把時刻 t的密切橢圓軌道根數表示為參考軌道根數同攝動項之和。攝動項分為短周期項、長周期項和長期項。一般以地球引力位球諧函式展開式的二次帶諧係數作為一階小量,而按所達到的精度分為一階解和二階解。這種解法通稱為分析法。由於分析法公式較煩,近年來一般都採用數值積分法直接解衛星運動方程,或者採用半分析法與數值積分法相結合的方法,即短周期攝動用分析法計算,長期和長周期攝動用數值積分法計算。
地球引力位通常以球諧函式展開式表示,球諧函式的係數稱為地球引力場參數,其中同經度無關的係數稱為帶諧係數,同經度有關的係數稱為田諧係數。利用這些參數同觀測數據(方向、距離、距離差、距離變率和衛星至海洋面的高)之間的關係組成觀測方程,就可以同時推求出測站的地心坐標,衛星軌道根數和地球引力場參數。由於觀測方程中含有大量的待定參數,所以通常把軌道根數和大地測量參數(引力場參數和測站地心坐標)分開解算。
地球引力位的帶諧部分主要引起衛星軌道的長期和周期攝動,田諧部分只產生幅度較小的短周期攝動。從衛星運動理論知道,地球引力位的偶次帶諧係數引起衛星軌道升交點赤經和近地點角距的長期攝動,奇次帶諧係數引起軌道偏心率和傾角的長周期攝動。故一般根據長期觀測所獲得的升交點赤經和近地點角距的變化推求偶次帶諧係數,而根據軌道偏心率和傾角的變化推求奇次帶諧係數。計算時必須事先消除非地球引力場的各種攝動因素的影響。為了削弱觀測方程係數之間的相關性,須選取不同傾角的衛星進行觀測,並須經過一定時間的觀測,積累幾個月或幾個星期的衛星觀測數據,這樣就可單獨求定帶諧係數。
田諧係數的求定比較困難,因為它們引起的攝動周期較短,振幅也較小。只有由全球分布均勻的若干測站,對不同軌道的衛星進行精密觀測,才能求定田諧係數。這時觀測方程中,帶諧係數一般可作為已知參數;待定參數除了田諧係數外,還包括測站坐標和衛星軌道根數等項。
由於衛星觀測數據目前只能反映地球引力場的全球特徵,而地面重力測量數據可提供引力場的精細結構,所以只有把兩種觀測數據綜合解算,才能求得地球引力場比較精確的模型。
觀測衛星的方法 按其內容有:以恆星為背景測量衛星方向,人造衛星雷射測距,都卜勒頻移測量定位,衛星雷達測高等。
以恆星為背景測量衛星方向 利用衛星反射的太陽光或衛星上反射鏡反射的雷射束進行攝影,通過像片處理歸算,即可求得攝影瞬間衛星所在的空間方向。由攝影測量求得的衛星方向的精度,在良好的條件下可以達到±0.3″。
方向觀測法是60年代主要使用的方法,它的觀測數據曾用於幾何法建立空間三角網。由於觀測精度不易再提高,而且可供觀測的衛星和觀測的機會較少,所以已很少使用。
人造衛星雷射測距 用安置在地面站的衛星雷射測距儀向衛星發射雷射脈衝,並接收由衛星反射鏡反射回來的脈衝,測量脈衝往返所經過的時間,從而計算測站至衛星的距離。60年代初,曾試驗用雷射技術測量從地面站到月球的距離。利用月面漫反射進行測距的嘗試,未能取得令人滿意的結果。以後隨著帶雷射反射鏡的人造衛星的出現,以及儀器的改進,測距精度不斷提高。第一代雷射測距儀用目視跟蹤觀測,測距誤差為±2米;第二代為自動跟蹤,誤差為分米級;第三代的測距儀精度達到厘米級。 人造衛星雷射測距儀的工作原理如圖3。固體雷射器所發射的雷射脈衝,由取樣電路截取其極小部分能量,經光電轉換後形成一個基準信號,送至測時裝置,作為計時的開門脈衝。雷射脈衝的大部分由光學系統發射至衛星。衛星上的反射鏡將脈衝反射回到地面,為接收系統所接收,並由光電倍增管轉換為電脈衝,經放大、整形後送至測時裝置作為計時的關門脈衝。雷射脈衝往返於測距儀與衛星間的傳播時間,由計數器記錄下來,據以計算出測距儀至衛星的距離。
衛星雷射測距儀分為固定式和流動式兩類。前者安裝在地面的固定測站上,後者可安裝在車輛上,具有高度機動性。兩類測距儀的精度大致相同。
為了用計算機控制雷射測距儀,使它自動跟蹤衛星,須有精確的軌道預報。根據預報數據換算成觀測時衛星的坐標,再計算出衛星的方位角、高度角和距離。輸入計算機進行自動控制,跟蹤衛星。
人造衛星雷射測距技術已被廣泛地套用於大地測量和地球動力學。70年代,地球和月球之間距離的測定有很大進展。月球雷射測距除起到與衛星雷射測距相同的作用外,還可以改善月球星曆,推求地球引力參數GM。月球雷射測距精度已達到±10厘米左右。
都卜勒頻移測量定位 都卜勒頻移測量的原理以都卜勒效應為基礎。裝在衛星上的無線電發射機連續發射的電磁波頻率為fs,地面站接收機所接收到的電磁波頻率為fe。由於衛星對地面站的相對運動,根據都卜勒效應有下列關係:
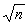
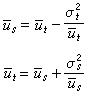
子午衛星系統,也稱海軍導航衛星系統(NNSS),就是利用都卜勒測量原理進行導航和定位的一種典型的系統。該系統的子午衛星不斷發射供都卜勒頻移測量用的電磁波信號,頻率分別為150和400兆赫,在 400兆赫載波上調製有時間信號和計算衛星空間位置用的“廣播星曆”。地面測站上的都卜勒接收機在觀測都卜勒頻移的同時,也接收這些信息。利用觀測到的都卜勒頻移,以及衛星的瞬間位置和測站坐標之間的數學關係,可以計算出測站的地心坐標。用以進行子午衛星都卜勒測量的儀器稱為都卜勒接收機。
地面測站大約每隔一小時可以觀測到子午衛星通過一次。一般觀測40~50次,利用廣播星曆和單點定位技術求得的測站地心坐標,其精度約為±3~±5米。此外還可採用聯測定位技術(在兩個測站上對子午衛星進行同步觀測)和短弧定位技術(多測站上對子午衛星進行同步觀測)。這兩種定位技術都可以削弱衛星的星曆誤差和大氣折射的影響,但前者將衛星廣播星曆視為已知值,後者則將它作為觀測量處理。採用這兩種技術按廣播星曆計算,可將每兩點之間相對位置的誤差減小到 1米以內。美國還於事後計算1~2顆子午衛星的精密星曆。根據這種星曆和單點定位技術計算的測站地心坐標的誤差也在±1米以內。
子午衛星都卜勒定位法不受天氣影響,所用儀器輕,操作簡便,現在已成為測定地麵點地心坐標的主要方法。在天文大地網中,適當地測設都卜勒測站,可以檢核和改善網的質量,並把局部大地坐標系轉換為全球統一的地心坐標系。衛星都卜勒定位和地面水準測量結合,還可得出精度優於1米的相對高程異常。
衛星雷達測高 由星載雷達測高儀向海洋表面垂直發射電脈衝,這些脈衝被海洋表面反射,衛星接收到這些信號後,由計時系統自動記錄脈衝往返的時間,據此即可計算衛星至瞬時海洋表面的垂直距離。由於脈衝束的發散和脈衝寬度的影響,所求得的高為一小塊圓形區域內的平均高。據試驗表明,“吉奧斯” 3號的測高精度為±0.6米,“海洋衛星”1號已將此精度提高到±0.1米。
發展趨勢 衛星大地測量雖然在短短20多年中取得了很大的成就,但在理論、觀測方法和觀測精度等方面,都還有待於進一步提高和完善。目前正在發展中的衛星大地測量新技術有以下4個方面:
①全球定位系統 (GPS)。這一系統是在子午衛星定位系統的基礎上發展起來的。它將包含18顆衛星,軌道高度為20000公里,傾角為55°。衛星分布在升交點相距120°的3個軌道面內。這樣在地球上任何地點和任何時刻,至少能同時觀測到4顆衛星,達到了連續定位的要求。衛星發射兩種頻率的電磁波,分別為1227.6和1575.4兆赫,在載波上調製有精確的時間信息和衛星軌道數據。全球定位系統的定位原理同子午衛星系統不完全相同,全球定位系統的衛星上帶有精確的原子鐘,所發出的時間信息和頻率很穩定,它是以衛星到地面站的時間信號所經歷的時間作為觀測量,換算為距離後確定點位。因此接收機內時間系統也要求有較高的精度。1983年已有7顆全球定位衛星在軌道上運行。
②衛星射電干涉測量系統(GPS/VLBI)。觀測河外類星體射電源的甚長基線干涉測量技術。由於觀測目標非常遙遠,信號微弱,因此接收天線和儀器設備龐大而複雜,費用昂貴,而且只能在少數固定台站上使用。近年來,研究試驗以全球定位系統的衛星信號為射電源的干涉測量系統,已取得令人鼓舞的結果。這個系統的接收天線和處理設備比較輕便簡單,為大地測量開闢了嶄新的途徑。
③衛星重力梯度測量。在衛星上安裝重力梯度儀,由梯度測量獲取地球重力場信息。此法適用於局部大地水準面的測定,精度達到米級。對於尚未測量的地區和困難地區可用此法測定大地水準面。
④ 衛星-衛星跟蹤技術。由地面跟蹤站觀測高軌道上的衛星(如軌道高度為35800公里的“套用技術”衛星ATS-6),並精確定軌,由這顆衛星跟蹤一個低軌道上的衛星(如高度為850公里的“吉奧斯”3號或高度為240公里的“阿波羅”太空飛行器),進行距離變化率測量。這是一種高-低衛星跟蹤方法。另外還有低-低衛星跟蹤方法,即兩個相距 200公里的衛星在同一個低軌道上進行跟蹤。
衛星-衛星跟蹤已經作過多次試驗,獲得了初步成果,目前正在改進中。