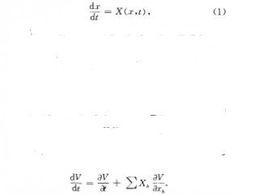簡介
李亞普諾夫第二方法是通過尋找滿足某種幾何性質的函式值直接推證方程組穩定性的一種方法。
李亞普諾夫第二方法就是藉助於一個所謂李亞普諾夫函式V(x,t)及根據微分方程所計算得到的V沿著軌線的導數dV/dt的符號性質來直接推斷穩定性問題。
具體內容
李亞普諾夫第二方法考慮實方程組 這裡X在集Ω(A,τ):||x||≤A,t≥τ上連續且滿足局部李普希茨條件，且當t≥τ時，X(0;t)≡0。
李亞普諾夫第二方法設數量函式V(x,t)及W(x)分別在Ω(A,τ)及Ω(A)中有定義且連續，對於t≥τ有V(0,t)≡0及W(0)=0，V(x,t)在Ω(A,τ)內稱為常正的（常負的），如果它在此集中≥0（≤0）；W(x)在Ω(A)內稱為定正的（定負的），如果對於x≠0，它在Ω(A)內均>0（<0）；V(x,t)在Ω(A,τ)內稱為定正的（定負的），如果它在該集中不小於（不大於）定正（定負）函式W(x)。如果進一步要求V(x,t)為C 函式，則它沿著實向量方程組的軌線的導數為
函式V(x,t)稱為Ω(A,τ)上的李亞普諾夫函式，如果它在該集中是定正的，且dV/dt為常負的。
定理
下面敘述李亞普諾夫給出的幾個定理：
1.(穩定性定理)如果存在定義於Ω(A,τ)上的李亞普諾夫函式V(x,t)，則原點是穩定的；
2.(漸近穩定性定理)如果在Ω(A,τ)內有一個不大於定正函式W(x)的李亞普諾夫函式V(x,t)，並使dV/dt為定負，則原點是漸近穩定的；
3.(不穩定性定理)設U(x,t)為定義於Ω(A,τ)上的有界C 函式，在Ω的某一子域Ω內U>0，Ω的邊界的一部分B包含射線T:x=0，t≥τ，且在B上U=0。假定下列條件成立，則原點是不穩定的：
1)只要t≥τ，就有點(x,t)∈Ω任意接近T；
2)對於每一個小的h>0，有k(h)>0，使得在Ω內U≥h蘊涵在Ω內U'≥k(h)。
