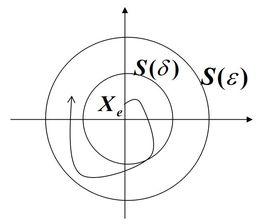基本概念
李亞普諾夫穩定性
李亞普諾夫方程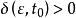
李亞普諾夫方程
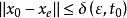李亞普諾夫方程在1892年，俄國數學家李亞普諾夫（Lyapunov）提出將判定系統穩定性的問題歸納為兩種方法：李亞普諾夫第一法和李亞普諾夫第二發 ，都對應存在另一實數 ，使當 時，從任意初始狀態x0齣發的解都滿足：
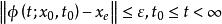李亞普諾夫方程
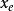李亞普諾夫方程則稱平衡狀態 為李亞普諾夫意義下穩定。
李亞普諾夫第二法
李亞普諾夫第一法又稱間接法，是利用系統狀態方程的解來判定穩定性，需要引入線性近似並求解方程。
相比之下，李亞普諾夫第二法（又稱直接法）直接從系統運動方程出發，通過構造李亞普諾夫函式，並分析它和它的一次導數的符號特性來獲得系統穩定性的有關信息。
李亞普諾夫方程就是從直接法中推導而來的一個線性定常系統穩定性判據方程。
李亞普諾夫方程
形式為，
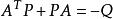李亞普諾夫方程這個方程作為穩定判據表示的是，對於沒有外部輸入的線性定常連續系統，其原點平衡狀態漸進穩定的充分必要條件為： 對於任意給定的正定對稱矩陣Q，有唯一的正定對稱矩陣P使李亞普諾夫矩陣方程成立 。
判定和使用方法
穩定性判定
使用李亞普諾夫第二法的條件是構造李亞普諾夫函式V(x)，該函式是定義的一個正定標量函式，作為虛構的廣義能量函式。
對於一個給定系統，若能找到V(x)是正定的，而其一階導數是負定的，則這個系統是漸進穩定（漸進穩定是指在李亞普諾夫穩定的前提下，時間趨於無窮時，系統能夠達到穩定狀態）的。
對於線性定常系統，可以利用李第二法相關定理導出簡化判據，即李亞普諾夫方程判據。
構造函式
如果得到了李亞普諾夫方程，
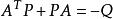李亞普諾夫方程則李亞普諾夫函式可以構造為：
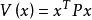李亞普諾夫方程也就可以通過李函式對系統的穩定性進行分析。
Matlab求解
在Matlab軟體中，使用X=lyap(A,C)可以求解滿足李雅普諾夫方程的對稱矩陣X；離散系統可用X=dlyap(A,C)求解對稱矩陣X。
