Prim算法:普里姆算法（Prim算法），圖論中的一種算法，可在加權連通 -百科知識中文網

Prim算法

普里姆算法（Prim算法），圖論中的一種算法，可在加權連通圖里搜尋最小生成樹。意即由此算法搜尋到的邊子集所構成的樹中，不但包括了連通圖裡的所有頂點（英語：Vertex (graph theory)），且其所有邊的權值之和亦為最小。該算法於1930年由捷克數學家沃伊捷赫·亞爾尼克（英語：Vojtěch Jarník）發現；並在1957年由美國計算機科學家羅伯特·普里姆（英語：Robert C. Prim）獨立發現；1959年，艾茲格·迪科斯徹再次發現了該算法。因此，在某些場合，普里姆算法又被稱為DJP算法、亞爾尼克算法或普里姆－亞爾尼克算法。

基本信息

中文名：Prim算法
英文名：Prim Algorithm
別稱：最小生成樹算法
類型：算法
提出者：沃伊捷赫·亞爾尼克（Vojtěch Jarník）

提出時間：1930年
套用學科：計算機，數據結構，數學（圖論）
適用領域範圍：套用圖論知識的實際問題
算法：貪心

算法描述

1).輸入：一個加權連通圖，其中頂點集合為V，邊集合為E；

2).初始化：V = {x}，其中x為集合V中的任一節點（起始點），E = {},為空；

3).重複下列操作，直到V = V：

a.在集合E中選取權值最小的邊<u, v>，其中u為集合V中的元素，而v不在V集合當中，並且v∈V（如果存在有多條滿足前述條件即具有相同權值的邊，則可任意選取其中之一）；

b.將v加入集合V中，將<u, v>邊加入集合E中；

4).輸出：使用集合V和E來描述所得到的最小生成樹。

時間複雜度

最小邊、權的數據結構	時間複雜度（總計）
鄰接矩陣、搜尋	O(V^2)
二叉堆（後文偽代碼中使用的數據結構）、鄰接表	O((V + E) log(V)) = O(E log(V))
斐波那契堆、鄰接表	O(E + V log(V))

通過鄰接矩陣圖表示的簡易實現中，找到所有最小權邊共需O（V）的運行時間。使用簡單的二叉堆與鄰接表來表示的話，普里姆算法的運行時間則可縮減為O(ElogV)，其中E為連通圖的邊數，V為頂點數。如果使用較為複雜的斐波那契堆，則可將運行時間進一步縮短為O(E+VlogV)，這在連通圖足夠密集時（當E滿足Ω（VlogV）條件時），可較顯著地提高運行速度。

圖例描述

圖例	說明	不可選	可選	已選（V）
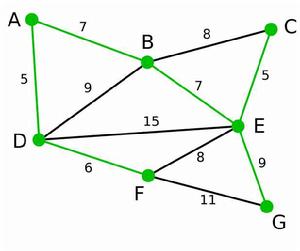
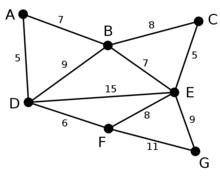Prim算法	此為原始的加權連通圖。每條邊一側的數字代表其權值。	-	-	-
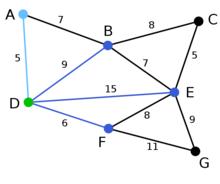Prim算法	頂點D被任意選為起始點。頂點A、B、E和F通過單條邊與D相連。A是距離D最近的頂點，因此將A及對應邊AD以高亮表示。	C, G	A, B, E, F	D
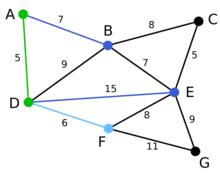Prim算法	下一個頂點為距離D或A最近的頂點。B距D為9，距A為7，E為15，F為6。因此，F距D或A最近，因此將頂點F與相應邊DF以高亮表示。	C, G	B, E, F	A, D
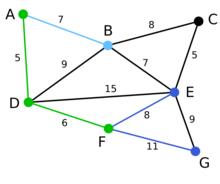Prim算法	算法繼續重複上面的步驟。距離A為7的頂點B被高亮表示。	C	B, E, G	A, D, F
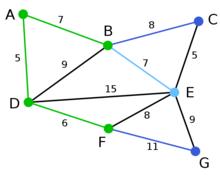Prim算法	在當前情況下，可以在 C、 E與 G間進行選擇。 C距 B為8， E距 B為7， G距 F為11。點 E最近，因此將頂點 E與相應邊 BE高亮表示。	無	C, E, G	A, D, F, B
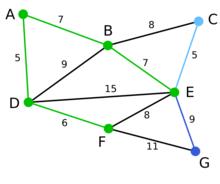Prim算法	這裡，可供選擇的頂點只有C和G。C距E為5，G距E為9，故選取C，並與邊EC一同高亮表示。	無	C, G	A, D, F, B, E
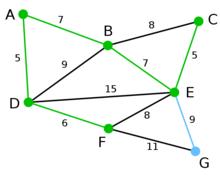Prim算法	頂點G是唯一剩下的頂點，它距F為11，距E為9，E最近，故高亮表示G及相應邊EG。	無	G	A, D, F, B, E, C
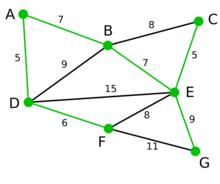Prim算法	現在，所有頂點均已被選取，圖中綠色部分即為連通圖的最小生成樹。在此例中，最小生成樹的權值之和為39。	無	無	A, D, F, B, E, C, G