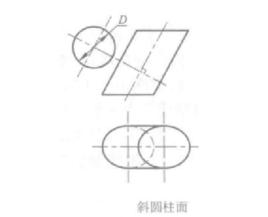
表面積
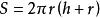 斜圓柱
斜圓柱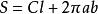 斜圓柱
斜圓柱圓柱的全面積是刻畫圓柱表面積大小的一個數量及其計算公式。 直 圓柱的側面積與底面積的和為它的全面積。如果直圓柱的底面半徑為r,高為h,那么它的全面積為 。 斜圓柱的側面積和它的兩底橢圓面積的和是它的全面積。設母線長為l,直截面網周長為C,底面橢圓的長短半軸為a、b,斜圓柱全面積為 。
正截面
與柱面軸線垂直的截平面稱為 正截面,如圖10一10所示.正截面與柱面的截交線(稱 正 截交線)為圓,則柱面為 圓柱面(迴轉圓柱面),圓柱面的軸線垂直於圓柱底面時,稱為 正圓柱 面。如圖10一10a所示。圓柱面的軸線傾斜於圓柱底面時,稱為 斜圓柱面,圖10一lOb所示的斜圓柱底面形狀為橢圓,如正截交線為橢圓,則稱為 橢圓柱面,橢圓柱面的軸線垂直於柱底時,稱為 正橢圓柱面,如圖10一l0ce所示。橢圓柱面的軸線傾斜於橢圓柱底面時,稱為 斜橢圓 柱面,如圖10—10d所示。
正截面與柱面截交線的實形可用變換投影面法求得。如圖10一lOd所示,作一垂直於軸線的正截面P,平面P與柱面的交線實形為橢圓(其長軸等於導圓的直徑D),因此這個柱面為橢圓柱面。
 圖2(a)
圖2(a)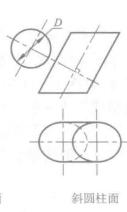 圖2(b)
圖2(b) 圖2(c)
圖2(c)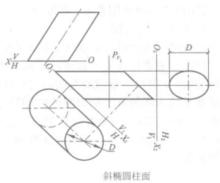 圖3
圖3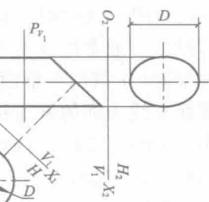 圖3(a)
圖3(a)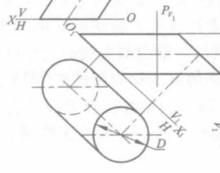 圖3(b)
圖3(b)求截交線
求平面與斜圓柱的截交線
例1 求平面P與斜圓柱的截交線( 素線法),如圖4(a)所示。
解:分析:斜圓柱被正垂面P切割。斜圓柱的柱面的V、H投影無積聚性,故其截交線上的一般點的求解只能用 素線法來求解。
作圖:如圖4(b)所示。
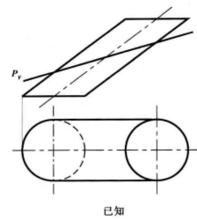 圖4(a)
圖4(a)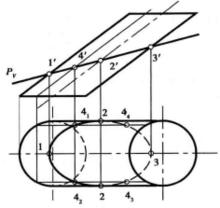 圖4(b)
圖4(b) 斜圓柱
斜圓柱 斜圓柱
斜圓柱 斜圓柱
斜圓柱 斜圓柱
斜圓柱 斜圓柱
斜圓柱 斜圓柱
斜圓柱 斜圓柱
斜圓柱① 求特殊點:求橢圓長、短軸的端點 和 (前後兩條素線上的特殊點都以 點表示)。 與圓柱正面投影輪廓素線的交點1’、3’,是橢圓長軸端點 、 的正面投影; 與圓柱最前、最後素線的正面投影的交點為2’,由此求出長短軸端點的水平投影1、2(注意前後共有兩個點)、3。
 斜圓柱
斜圓柱② 求一般點:為使作圖準確,還需要再求出屬於截交線的若干個一般點。例如在截交線正面投影上任取一點4'。4’是橢圓上一般點的正面投影,我們採用對稱的方式來求解Ⅳ點在H面4個位置上的投影。根據橢圓是對稱圖形,可作出 四個點。
③ 連點:在H投影面上用光滑的曲線依次連線各點,即得截交線的水平投影。
判別可見性:由圖可知截交線以短軸為分界線,左半部分為可見,右半部分為不可見。
斜圓柱體展開
1) 做出斜圓柱的主視圖。把斜圓柱兩邊素線點標為A、C、B、D(見圖5,圖5(b)、(c)是圖5(a)的放大圖)。
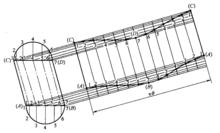 圖5(a))
圖5(a))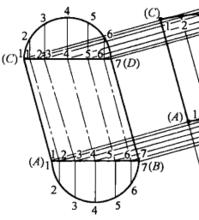 圖5(b)
圖5(b)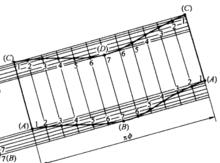 圖5(c)
圖5(c)2) 分別做斜圓柱上端線段AB和下端線段CD的半圓,並把半圓六等分,過上下兩半圓等分點做垂線,上半圓等分點垂線垂直於線段CD,下半圓等分點垂線垂直於線段AB,線上段CD與線段AB上對應得交點1、2、3、4、5、6、7點。用線段把上下1、2、3、4、5、6、7點對應相連。
3) 過斜主視圖上下1、2、3、4、5、6、7點向右引十四條平行線,平行線與斜圓柱素線AC與BD垂直。截取上邊1點平行線的長等於斜圓柱圓的周長,並做十二等分,過等分點做平行線的垂線,與十四條平行線對應相交,上下同時對應得交點為1、2、3、4、5、6、7、6、5、4、3、2、1點。用曲線分別把上下的交點順次圓滑相連,即得到 斜圓柱的展開圖。