數論格線求積分法

J(ƒ，p(k))就是由點集p(k)(1≤k≤n )的偏差小，而且要求p(k)的形式簡單，易於計算。 也就是說用點集Q(k)(1≤k≤p)構造的求積公式有誤差。

數論格線求積分法

正文

高維數值積分數論方法研究開始於20世紀50年代末，其理論基礎是數論中的一致分布論。命Us表示 s維單位立方體。假定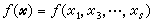是Us上定義的函式,並假定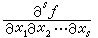存在且其絕對值以C為界。命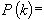 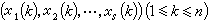是Us中具有偏差D(n)的點集。所謂數論方法就是用被積函式在p(k) (1≤k≤n)上值的算術平均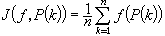

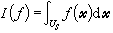
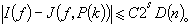
作為Us上定積分

的近似值，而誤差由下面的公式給出：

J(ƒ，p(k))就是由點集p(k)(1≤k≤n)定義的一個求積公式。因此尋求Us上最佳求積公式的問題即等價於尋求Us上最佳偏差的點集的問題。從計算方法的觀點看，不僅要求點集p(k)(1≤k≤n)的偏差小，而且要求p(k)的形式簡單，易於計算。
① 科羅博夫-勞卡方法　命p表示素數,a=(α1,α2,…,αs)表示整數向量，科羅博夫和E.勞卡證明了,對於任意p，皆存在a，使點集

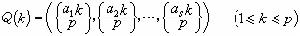
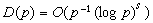有偏差。也就是說用點集Q(k)(1≤k≤p)構造的求積公式有誤差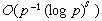。對於p求出a的計算量為O(p2)次初等運算。因此當p較大時,算出a來很困難。
② 分圓域方法　分圓域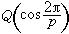是一個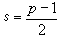次代數數域。利用 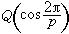的獨立單位組可得它的一個適合於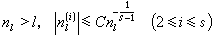

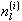的單位列nl(l＝1,2,…),其中表示nl的共軛數。如果使

則得點集

用這一點集構造的求積公式的誤差為

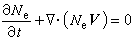
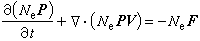式中ε為任意正數。算出nl、hjl(1≤j≤s-1)的計算量為O(lognl)。因此算出nl和沒有困難，但缺點是誤差略為偏大些。
當2≤s≤18時，上述的p、a、nl和h都已彙編成表，可供查閱。
數論方法得到的求積公式的誤差主階均與維數無關，所以當s較大時，用數論方法近似計算Us上的定積分比較合算。
參考書目
　華羅庚、王元著：《數論在近似分析中的套用》，科學出版社，北京，1978。

配圖

相關連線