基本介紹
 數乘向量
數乘向量 數乘向量
數乘向量 數乘向量
數乘向量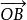 數乘向量
數乘向量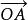 數乘向量
數乘向量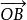 數乘向量
數乘向量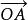 數乘向量
數乘向量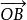 數乘向量
數乘向量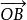 數乘向量
數乘向量數乘向量:(1)對於向量 a= 與實數k,在兩點O,A所確定的直線上取一點B,使有向線段 與 的數量之比等於k(當k>0時, 與 同向;當k<0時, 與 反向;當k=0時, = 0),這時向量 b= 用 b=k a表示,這種運算稱為向量的 數量乘法,簡稱數乘,向量b稱為數k與向量 a的乘積。
(2)實數λ與向量 a的乘積λ a是一個向量,它的模為|λ a|=|λ|·| a|;λ a的方向,當λ>0時與 a同向,當λ<0時與 a反向,當λ=0時有λ a= 0,我們把這種運算稱為數乘向量。
特別地,當λ =-1時,記(-1) a =- a。
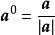 數乘向量
數乘向量由定義知λ a與 a是共線向量,任意非零向量 a都可寫作a=| a| a ,或 。這說明非零向量 a乘以它的模的倒數,便可得到與它同方向的單位向量 a ,簡稱為把 a單位化 。
數乘向量的相關性質
數量與向量的乘法滿足如下的運算規律:
(1) 1· a= a;
(2)結合律:λ(μ a) = (λμ) a;
(3)第一分配律:(λ+μ) a=λ a+μ a;
(4)第二分配律:λ( a+ b)=λ a+λ b。
其中, a, b為任意向量,λ,μ為任意實數。
證明:(1),(2)根據定義直接驗證。
(3)如果 a = 0或λ,μ,λ+μ中至少有一個為零,那么等式顯然成立,因此只需證明當 a≠ 0,λμ≠0,λ+μ≠0的情形。
①如果λμ>0,則(λ+μ) a,λ a, μ a同向,因此有
|(λ+μ) a|=|λ+μ|| a|=(|λ|+|μ|)| a|=|λ|| a|+|μ||a|=|λ a|+|μ a|=|λ a+μ a|,
所以有(λ+μ) a=λ a+μ a。
②如果λμ<0,不失一般性,不妨設λ>0,μ<0,再討論λ+μ>0和λ+μ<0兩種情形。下面只證明前一種情形。
設λ>0,μ<0,λ+μ>0,這時-μ>0,因λ+μ>0,由①有:
(λ+μ) a+(-μ) a=[(λ+μ)+(-μ)] a=λ a,
所以(λ+μ) a=λ a-(-μ) a =λ a+μ a。
(4)如果λ=0或 a, b之中有一個為0,等式顯然成立。
下面證明λ≠0, a≠ 0, b≠ 0。
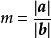 數乘向量
數乘向量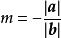 數乘向量
數乘向量①若 a, b共線,當 a, b同向時,取 ;當 a, b反向時,,
顯然有 a=m b。於是有
λ( a+ b)=λ(m b+ b)=λ[(m+1) b]=[λ(m+1)] b=(λm+λ) b=(λm) b+λ b=λ(m b)+λ b=λ a+λ b.
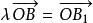 數乘向量
數乘向量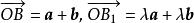 數乘向量
數乘向量②若 a, b不共線,如圖1所示,顯然由 a, b為兩邊構成的△OAB與由a,b為兩邊構成的△OA₁B₁相似,因此對應的第三邊所成向量滿足,因,所以λ( a+ b)=λ a+λ b。
從向量加法與數乘向量的運算規律知,對於向量也可以像實數與多項式那樣去運算 。
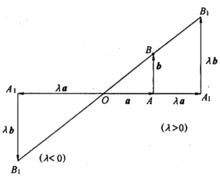 圖1
圖1