群公理
容易驗證模n互質同餘類在乘法運算下滿足阿貝爾群的公理。
恆同: 1 是恆同；
閉：如果a和b都與n互質，那么ab也是；
逆：找x滿足ax≡ 1 (modn) 等價於解ax+ny= 1，可用歐幾里得算法求出；
結合性和交換性：由整數的相應事實以及模n運算是一個環同態推出。
記法
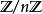整數模n乘法群
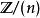整數模n乘法群
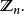整數模n乘法群
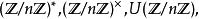整數模n乘法群整數模n環記作 或 （即整數環模去理想n Z= (n) ，由n的倍數組成）或 因作者所喜，它的單位群可能記為 或類似的記號。
結構
2 的冪次
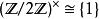整數模n乘法群模 2 只有一個互質同餘類 1，所以 平凡。
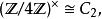整數模n乘法群模 4 有兩個互質同餘類，1 和 3，所以 兩元循環群。
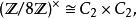整數模n乘法群模 8 有四個互質同餘類，1, 3, 5 和 7，每個平方都是 1，所以 Klein 四元群。
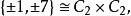整數模n乘法群
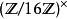整數模n乘法群
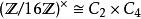整數模n乘法群模 16 有八個互質同餘類，1, 3, 5, 7, 9, 11, 13 和 15。 為 2-扭子群（即每個元素的平方為 1），所以 不是循環群。3的冪次：1,3,9,11 是一個 4 階子群，5 的冪次也是，1,5,9,13。所以 。
奇質數的冪
對奇質數的冪p，此群是循環群：
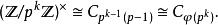整數模n乘法群一般合數
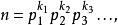整數模n乘法群 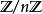整數模n乘法群中國剩餘定理說明如果 那么環 每個質數冪因子相應的環的直積：
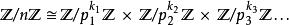整數模n乘法群
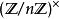整數模n乘法群類似地， 的單位群是每個質數冪因子相應群的直積：
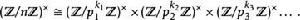整數模n乘法群階數
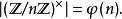整數模n乘法群群的階數由歐拉函式給出： （OEIS中的數列A000010） 這是直積中各循環階數的乘積。
指數
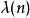整數模n乘法群
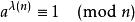整數模n乘法群指數為卡麥可函式，（OEIS中的數列A002322），即這些循環群的階數的最低公倍數。這意味著如果a和n互質， 。
生成元
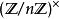整數模n乘法群
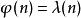整數模n乘法群是循環群若且唯若 。這在n為奇質數的冪次、奇質數冪次 2 倍、2 和 4 成立，此時也稱一個生成元為 模 n 的原根。
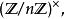整數模n乘法群 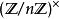整數模n乘法群 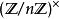整數模n乘法群因為所有 n= 1, 2, ..., 7 是循環群，上述結論的另一種說法是：如果n< 8 那么 有原根；如果n≥ 8，且不能被 4 或者兩個不同的奇質數整除， 有原根。( A033948= 1, 2, 3, 4, 5, 6, 7, 9, 10, 11, 13, 14, 17, 18, 19, 22, 23, 25, 26, 27, 29, 31, 34, 37, 38, 41, 43, 46, 47, 49, 50, ... )
一般情形每個直積因子循環有一個生成元。
