散列表(Hash table,也叫哈希表),是根據關鍵碼值(Key value)而直接進行訪問的數據結構。也就是說,它通過把關鍵碼值映射到表中一個位置來訪問記錄,以加快查找的速度。這個映射函式叫做散列函式,存放記錄的數組叫做散列表。
基本概念
若結構中存在關鍵字和K相等的記錄,則必定在f(K)的存儲位置上。由此,不需比較便可直接取得所查記錄。稱這個對應關係f為散列函式(Hash function),按這個思想建立的表為散列表。
對不同的關鍵字可能得到同一散列地址,即key1≠key2,而f(key1)=f(key2),這種現象稱衝突。具有相同函式值的關鍵字對該散列函式來說稱做同義詞。綜上所述,根據散列函式H(key)和處理衝突的方法將一組關鍵字映象到一個有限的連續的地址集(區間)上,並以關鍵字在地址集中的“象”作為記錄在表中的存儲位置,這種表便稱為散列表,這一映象過程稱為散列造表或散列,所得的存儲位置稱散列地址。
若對於關鍵字集合中的任一個關鍵字,經散列函式映象到地址集合中任何一個地址的機率是相等的,則稱此類散列函式為均勻散列函式(Uniform Hash function),這就是使關鍵字經過散列函式得到一個“隨機的地址”,從而減少衝突。
常用的構造散列函式的方法
散列函式能使對一個數據序列的訪問過程更加迅速有效,通過散列函式,數據元素將被更快地定位
直接定址法:取關鍵字或關鍵字的某個線性函式值為散列地址。即H(key)=key或H(key) = a•key + b,其中a和b為常數(這種散列函式叫做自身函式)
數字分析法
平方取中法
摺疊法
隨機數法
除留餘數法:取關鍵字被某個不大於散列表表長m的數p除後所得的餘數為散列地址。即 H(key) = key MOD p, p<=m。不僅可以對關鍵字直接取模,也可在摺疊、平方取中等運算之後取模。對p的選擇很重要,一般取素數或m,若p選的不好,容易產生同義詞。
處理衝突的方法
開放定址法;Hi=(H(key) + di) MOD m, i=1,2,…, k(k<=m-1),其中H(key)為散列函式,m為散列表長,di為增量序列,可有下列三種取法:
1、di=1,2,3,…, m-1,稱線性探測再散列;
2、di=1^2, (-1)^2, 2^2,(-2)^2, (3)^2, …, ±(k)^2,(k<=m/2)稱二次探測再散列;
3、di=偽隨機數序列,稱偽隨機探測再散列。 ==
再散列法:Hi=RHi(key), i=1,2,…,k RHi均是不同的散列函式,即在同義詞產生地址衝突時計算另一個散列函式地址,直到衝突不再發生,這種方法不易產生“聚集”,但增加了計算時間。
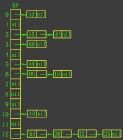
鏈地址法(拉鏈法)
建立一個公共溢出區
查找的性能分析
散列表的查找過程基本上和造表過程相同。一些關鍵碼可通過散列函式轉換的地址直接找到,另一些關鍵碼在散列函式得到的地址上產生了衝突,需要按處理衝突的方法進行查找。在介紹的三種處理衝突的方法中,產生衝突後的查找仍然是給定值與關鍵碼進行比較的過程。所以,對散列表查找效率的量度,依然用平均查找長度來衡量。
查找過程中,關鍵碼的比較次數,取決於產生衝突的多少,產生的衝突少,查找效率就高,產生的衝突多,查找效率就低。因此,影響產生衝突多少的因素,也就是影響查找效率的因素。影響產生衝突多少有以下三個因素:
散列函式是否均勻;
處理衝突的方法;
散列表的裝填因子。散列表的裝填因子定義為:α= 填入表中的元素個數 / 散列表的長度
α是散列表裝滿程度的標誌因子。由於表長是定值,α與“填入表中的元素個數”成正比,所以,α越大,填入表中的元素較多,產生衝突的可能性就越大;α越小,填入表中的元素較少,產生衝突的可能性就越小。
實際上,散列表的平均查找長度是裝填因子α的函式,只是不同處理衝突的方法有不同的函式。以下給出幾種不同處理衝突方法的平均查找長度: