概念
用關鍵字標識一個數據元素,查找時根據給定的某個值,在表中確定一個關鍵字的值等於給定值的記錄或數據元素。在計算機中進行查找的方法是根據表中的記錄的組織結構確定的。
順序查找也稱為線形查找,從數據結構線形表的一端開始,順序掃描,依次將掃描到的結點關鍵字與給定值k相比較,若相等則表示查找成功;若掃描結束仍沒有找到關鍵字等於k的結點,表示查找失敗。
二分查找要求線形表中的結點按關鍵字值升序或降序排列,用給定值k先與中間結點的關鍵字比較,中間結點把線形表分成兩個子表,若相等則查找成功;若不相等,再根據k與該中間結點關鍵字的比較結果確定下一步查找哪個子表,這樣遞歸進行,直到查找到或查找結束髮現表中沒有這樣的結點。
分塊查找也稱為索引查找,把線形分成若干塊,在每一塊中的數據元素的存儲順序是任意的,但要求塊與塊之間須按關鍵字值的大小有序排列,還要建立一個按關鍵字值遞增順序排列的索引表,索引表中的一項對應線形表中的一塊,索引項包括兩個內容:① 鍵域存放相應塊的最大關鍵字;② 鏈域存放指向本塊第一個結點的指針。分塊查找分兩步進行,先確定待查找的結點屬於哪一塊,然後在塊內查找結點。
哈希表查找是通過對記錄的關鍵字值進行運算,直接求出結點的地址,是關鍵字到地址的直接轉換方法,不用反覆比較。假設f包含n個結點,Ri為其中某個結點(1≤i≤n),keyi是其關鍵字值,在keyi與Ri的地址之間建立某種函式關係,可以通過這個函式把關鍵字值轉換成相應結點的地址,有:addr(Ri)=H(keyi),addr(Ri)為哈希函式。
順序查找
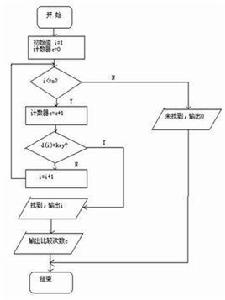
順序查找過程:從表中的最後一個記錄開始,逐個進行記錄的關鍵字與給定值進行比較,若某個記錄的關鍵字與給定值相等,則查找成功,找到所查的記錄;反之,若直到第一個記錄,其關鍵字和給定值比較都不相等,則表明表中沒有所查的記錄,查找失敗。
算法描述為
int Search(int d,int a[],int n)
{
/*在數組a[]中查找等於D元素,若找到,則函式返回d在數組中的位置,否則為0。其中n為數組長度*/
int i ;
/*從後往前查找*/
for(i=n-1;a!=d;--i)
return i ;
/*如果找不到,則i為0*/
}
二分查找
二分查找又稱折半查找,它是一種效率較高的查找方法。
【二分查找要求】:1.必須採用順序存儲結構2.必須按關鍵字大小有序排列。
【優缺點】折半查找法的優點是比較次數少,查找速度快,平均性能好;其缺點是要求待查表為有序表,且插入刪除困難。因此,折半查找方法適用於不經常變動而查找頻繁的有序列表。
【算法思想】首先,將表中間位置記錄的關鍵字與查找關鍵字比較,如果兩者相等,則查找成功;否則利用中間位置記錄將表分成前、後兩個子表,如果中間位置記錄的關鍵字大於查找關鍵字,則進一步查找前一子表,否則進一步查找後一子表。
重複以上過程,直到找到滿足條件的記錄,使查找成功,或直到子表不存在為止,此時查找不成功。
【算法複雜度】假設其數組長度為n,其算法複雜度為o(log(n))
下面提供一段二分查找實現的偽代碼:
BinarySearch(max,min,des)
mid-des then
max=mid-1
else
min=mid+1
return max
折半查找法也稱為二分查找法,它充分利用了元素間的次序關係,採用分治策略,可在最壞的情況下用O(log n)完成搜尋任務。它的基本思想是,將n個元素分成個數大致相同的兩半,取a[n/2]與欲查找的x作比較,如果x=a[n/2]則找到x,算法終止。如 果xa[n/2],則我們只要在數組a的右 半部繼續搜尋x。
分塊查找
分塊查找又稱索引順序查找,它是順序查找的一種改進方法。
方法描述:將n個數據元素"按塊有序"劃分為m塊(m ≤ n)。每一塊中的結點不必有序,但塊與塊之間必須"按塊有序";即第1塊中任一元素的關鍵字都必須小於第2塊中任一元素的關鍵字;而第2塊中任一元素又都必須小於第3塊中的任一元素,……。
操作步驟:
step1 先選取各塊中的最大關鍵字構成一個索引表;
step2 查找分兩個部分:先對索引表進行二分查找或順序查找,以確定待查記錄在哪一塊中;然後,在已確定的塊中用順序法進行查找。
哈希表查找
1 基本原理
我們使用一個下標範圍比較大的數組來存儲元素。可以設計一個函式(哈希函式, 也叫做散列函式),使得每個元素的關鍵字都與一個函式值(即數組下標)相對應,於是用這個數組單元來存儲這個元素;也可以簡單的理解為,按照關鍵字為每一個元素"分類",然後將這個元素存儲在相應"類"所對應的地方。
但是,不能夠保證每個元素的關鍵字與函式值是一一對應的,因此極有可能出現對於不同的元素,卻計算出了相同的函式值,這樣就產生了"衝突",換句話說,就是把不同的元素分在了相同的"類"之中。後面我們將看到一種解決"衝突"的簡便做法。
總的來說,"直接定址"與"解決衝突"是哈希表的兩大特點。
2 函式構造
構造函式的常用方法(下面為了敘述簡潔,設 h(k) 表示關鍵字為 k 的元素所對應的函式值):
a) 除余法:
選擇一個適當的正整數 p ,令 h(k ) = k mod p
這裡, p 如果選取的是比較大的素數,效果比較好。而且此法非常容易實現,因此是最常用的方法。
b) 數字選擇法:
如果關鍵字的位數比較多,超過長整型範圍而無法直接運算,可以選擇其中數字分布比較均勻的若干位,所組成的新的值作為關鍵字或者直接作為函式值。
3衝突處理
線性重新散列技術易於實現且可以較好的達到目的。令數組元素個數為 S ,則當 h(k) 已經存儲了元素的時候,依次探查 (h(k)+i) mod S , i=1,2,3…… ,直到找到空的存儲單元為止(或者從頭到尾掃描一圈仍未發現空單元,這就是哈希表已經滿了,發生了錯誤。當然這是可以通過擴大數組範圍避免的)。
4 支持運算
哈希表支持的運算主要有:初始化(makenull)、哈希函式值的運算(h(x))、插入元素(insert)、查找元素(member)。
設插入的元素的關鍵字為 x ,A 為存儲的數組。
初始化比較容易,例如
const empty=maxlongint; // 用非常大的整數代表這個位置沒有存儲元素
p=9997; // 表的大小
procedure makenull;
var i:integer;
begin
for i:=0 to p-1 do
A:=empty;
End;
哈希函式值的運算根據函式的不同而變化,例如除余法的一個例子:
function h(x:longint):Integer;
begin
h:= x mod p;
end;
我們注意到,插入和查找首先都需要對這個元素定位,即如果這個元素若存在,它應該存儲在什麼位置,因此加入一個定位的函式 locate
function locate(x:longint):integer;
var orig,i:integer;
begin
orig:=h(x);
i:=0;
while (ix)and(A[(orig+i)mod S]empty) do
inc(i);
//當這個循環停下來時,要么找到一個空的存儲單元,要么找到這個元
//素存儲的單元,要么表已經滿了
locate:=(orig+i) mod S;
end;
插入元素
procedure insert(x:longint);
var posi:integer;
begin
posi:=locate(x); //定位函式的返回值
if A[posi]=empty then A[posi]:=x
else error; //error 即為發生了錯誤,當然這是可以避免的
end;
查找元素是否已經在表中
procedure member(x:longint):boolean;
var posi:integer;
begin
posi:=locate(x);
if A[posi]=x then member:=true
else member:=false;
end;