簡介
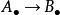 擬同構
擬同構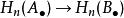 擬同構
擬同構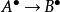 擬同構
擬同構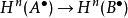 擬同構
擬同構擬同構是同調代數中的一個概念。鏈復形間的態射 被稱為擬同構,如果它所誘導的所有同調群間的同態 都是同構。上鏈復形間的態射 被稱為擬同構,如果它所誘導的所有上同調群間的同態 都是同構。
擬同構給出導出範疇中的同構。
同調代數
同調代數是數學的一個分支,它研究同調與上同調技術的一般框架。同調代數是一門相對年輕的學科,其源頭可追溯到代數拓撲(單純形同調)與抽象代數(合沖模)在十九世紀末的發展,這兩門理論各自由龐加萊與希爾伯特開創。
同調代數的發展與範疇論的出現密不可分。大致說來,同調代數是(上)同調函子及其代數結構的研究。“同調”與“上同調”是一對對偶的概念,它們滿足的範疇論性質相反(即:箭頭反向)。數學很大一部分的內在構造可藉鏈復形理解,其性質則以同調與上同調的面貌展現,同調代數能萃取這些鏈復形蘊含的資訊,並表之為拓撲空間、層、群、環、李代數與C*-代數等等“具體”對象的(上)同調不變數。譜序列是計算這些量的有力工具。
同調代數肇始即在代數拓撲中扮演要角。其影響日漸擴大,目前已遍及交換代數、代數幾何、代數數論、表示理論、運算元代數、偏微分方程與非交換幾何。K-理論是一門獨立的學科,它也採用同調代數的辦法。
導出範疇
導出範疇是同調代數中的一種構造。導出範疇的概念推廣並深化了傳統同調代數中導出函子的理論。這一構造是格羅滕迪克在20世紀60年代初提出的,他的學生讓-路易·韋迪耶在其指導下發展了相關理論。今天,導出範疇被廣泛套用於代數幾何和 D-模理論。
同構
在抽象代數中, 同構(英語:isomorphism)指的是一個保持結構的雙射。在更一般的範疇論語言中,同構指的是一個態射,且存在另一個態射,使得兩者的複合是一個恆等態射。
正式的表述是:同構是在數學對象之間定義的一類映射,它能揭示出在這些對象的屬性或者操作之間存在的關係。若兩個數學結構之間存在同構映射,那么這兩個結構叫做是 同構的。一般來說,如果忽略掉同構的對象的屬性或操作的具體定義,單從結構上講,同構的對象是完全等價的。
