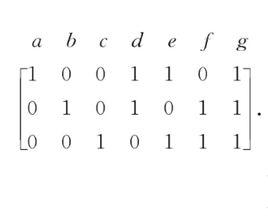基本介紹
法諾擬陣即二元擬陣F，僅含有7個元素，其表示矩陣為
法諾擬陣而其在投影平面上的圖像中，三個點位於同一條直線或同一條曲線上時，此三點構成F的相關集；否則為基。F不是單模擬陣，因此，以F為其子擬陣的擬陣也不是單模擬陣 。
性質介紹
引理1若擬陣M為正則的，則對於任何一個基礎，其基本矩陣是全單模的 。
一個二分的(但非正則的)擬陣的最簡單的例子，就是Fano擬陣。
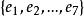法諾擬陣Fano擬陣其基礎集由7個元素組成，記為 ，圈的集合為
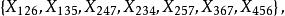法諾擬陣其中X={e|1≤t≤7，t≠i，j和k}，1≤i<j<k≤7。
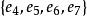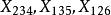法諾擬陣
法諾擬陣上述Fano擬陣的非正則性，可以按如下方式證明：因為容易驗證 為它的一個基礎。這時，它的三個基本圈為 ，其基本矩陣為
法諾擬陣其中x=±1，i≠j，1≤i，j≤4。假若此矩陣是全單模的，由於下面4個子陣的行列式
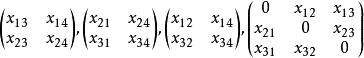法諾擬陣必須為偶數。從全單模性，又使得如下的方程．對於所有未知量，非1則-1，有解：
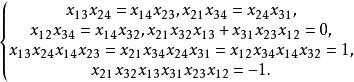法諾擬陣然而，這些方程將導致
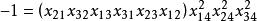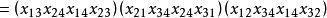法諾擬陣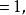
法諾擬陣
法諾擬陣因此，Fano擬陣不可能是全單模的，由引理1可知Fano擬陣是非正則的。
引理2 若一個擬陣M是正則的，則Fano擬陣和它的對偶均非M的次形。
引理3 若二分擬陣M是正則的，則它的基本矩陣在GF(2)上是X脫化的。
引理4 對於一個二分擬陣M，下面的說法是相互等價的：
(1) M在任何城上均為可表示的；
(2) M是可定向的；
(3) M是全單模的；
(4) M沒有次形與Fano擬陣或其對偶擬陣同構；
(5) M是X脫化的 。
