定義
設集合Q的元素是a、b、c，...，如果定義了兩個元素a、b的積，而且對於給定的a、c，存在唯一的b，使得ab=c，對於給定的b、c，存在唯一的a，使得ab=c，則稱Q關於所定義的二元合成法則構成一個 擬群。
相關概念與性質
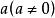擬群1. 體的概念可以用一些彼此不等價的方法轉移到非結合的情形上來。例如，可以考慮這樣的環，在其中，對於任意元素 和b，方程
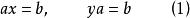擬群有解，但解不一定是唯一確定的。我們將稱任意這樣的環為 可除 環；從我們的定義可知，可除環可能有零因子。
一個可除環，如果在其中方程(1)的兩方程各有唯一解，這樣的可除環就叫作 擬體。擬體不能包含零因子，因而擬體的非零元關於乘法組成群胚，這就是 擬群，也就是一個群胚，在其中，對任意元素a和b，方程(1)的兩方程均唯一可解。
最後，我們將把術語體留來專指有單位元的擬體。體的非零元素依乘法組成有單位元的擬群，也就是 圈。
任意沒有零因子的(不一定結合的)環可嵌入擬體中。
2．存在不是體的擬體和不是圈的擬群，問題在於雖然擬群G中對任意元素a方程
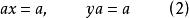擬群唯一可解，但這些解不一定相同，且不一定分別是G中其他元素的右或左單位元。
有單位元e的圈G之任意子擬群A是子圈，並以原來的e為單位元。
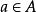擬群這是因為，對任意 ，方程(2)在G內有唯一解e，因而它也含於子擬群A中。
3．關於群的一系列結果可推廣到擬群，特別是可推廣到圈上。對此我們不去作進一步的討論，而只是引入同構的一個推廣，它在擬群理論中起著顯著的作用。
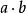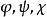擬群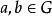
擬群
擬群設給定一有乘法 的群胚G，井設 是集G到自身上的任意一一映射，它們可以是相同的。若對任意 ，令
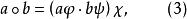擬群則在集G上我們得到一個新的群胚。這個新群胚不一定與原來的同構，但在某種程度上它們是相近的。
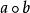擬群
擬群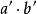
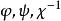擬群 擬群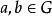
擬群 擬群與此相應地，有乘法 的群胚G稱為同形於有乘法 的群胚 ，若存在G到 上的三個一一映射 ，使得對任意 ，有
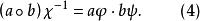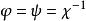擬群
擬群 擬群顯然，當 時，我們便得G到 上的同構映射。
易證，同形關係是自反的，傳遞的和對稱的。
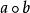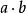擬群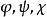 擬群 擬群在許多情形，為了方便，將認為兩運算 和 是在同一集M上給定的，而且認為(3)或(4)中的 是這個集到自身上的一一映射。
4．與擬群同形的任意群胚必是擬群。
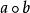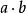擬群 擬群事實上，設在集G上給定一有乘法 的群胚和有乘法 的擬群，且知它們是同形的，也就是(3)成立。今證，例如，方程
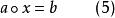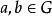擬群 擬群對任意 有唯一解。我們知道，方程
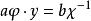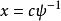擬群
擬群有唯一確定的解c。令 ，此時
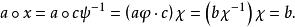擬群
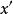擬群另一方面，若 是方程(5)的任一解，則
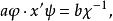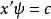擬群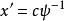
擬群
擬群從而 ，亦即 。
5．任意擬群同形於圈。
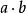擬群
擬群事實上，在有乘法 的擬群G中固定任意一個元素e，此時在G中存在一元素 ，使
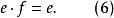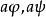擬群
擬群設a是G中任意元素，用 表示由下面方程唯一確定的元素，
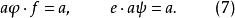擬群
擬群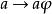
擬群
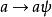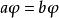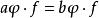擬群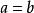
擬群
擬群映射 和 ，是集G到自身上的一一映射，其中a遍經整個集G。譬如，若 ，則 ，亦即 。
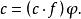擬群另一方面，若c是G中任一元素，則
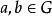擬群從而，對所有 ，令
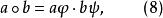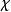擬群
擬群則在G上我們定義了一個新群胚，它與原來的擬群同形；在這裡恆等映射起 的作用，有人把這叫作 主向形。由上一款中證明過的知道，所得到的群胚是擬群，它還是圈，因為e是它的單位元。事實上，因為依(6)和(7)，
擬群故依(8)和(7)，
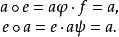擬群定理證完。
6．若有單位元的群胚同形於半群，則它們同構，因而兩者都是結合的且兩者都有單位元。
由此定理可得 Albert定理：若圈同形於群，則它們同構。特別，由此推知同形的群永遠同構，因此在群論中沒有必要使用同形概念。
擬群7．同形的概念也能轉移到非結合環的理論中去。考察一些有同一加群G的環，和上面一樣用等式(3)來定義環的同形，只是認定映射 是群G到自身上的同構映射，由上面得到的結果以及證明這些結果時利用的方法可以得出下面的一些結果：
同形於擬體的任意環本身也是擬體。
其他介紹
在數學中，特別是抽象代數裡， 擬群是一種類似於群的代數結構。擬群與群的相像之處是也能夠進行除法運算，但擬群中並沒有群所擁有的結合律。有單位元的擬群稱作 麼擬群或者 圈（loop）。
擬群的正規定義有兩種，分別帶有一種和三種二元運算。首先介紹第一種定義：
一個 擬群 (Q, *) 是一個集合Q 與一個二元運算 * 的結合（即一個原群），滿足對Q 中的任意元素a 和b，都存在唯一的Q 中元素x 和y，使得：
a*x =b ；
y*a =b。
這兩個唯一的元素被記作：x =a \b 和y =b /a。其中“\” 和 “/”分別表示被二元運算所定義的“左除法”和“右除法”。擬群的公理化需要用到存在量詞，因此也就需要建立在一階邏輯之上。
擬群的第二個定義是建立在泛代數的背景中。泛代數希望代數結構為簇，也就是說其公理化過程應該只需要到等式的概念。在這樣的要求下，擬群被定義為：
一個 擬群 (Q, *, \, /) 是一種 (2,2,2) 代數，其滿足等式:
y = x * (x \y) ；
y = x \(x * y) ；
y = (y /x) * x ；
y = (y * x) /x。
因此如果 (Q, *) 是依據第一種定義的擬群，那么 (Q, *, \, /) 則是其在泛代數範疇內對應的概念。
一個有單位元的擬群稱為一個 麼擬群或一個 圈，這裡的單位元是指Q 中元素e 使得：
x*e =x =e*x。
可以證明單位元e 是唯一的，並且這時每一個Q 中元素都有唯一的一個左逆元和右逆元。
拉丁方
一個有限擬群的乘法構成的乘法表是一個拉丁方：一個n ×n 的表格，每行每列都是 n 個不同的元素的排列，並且每個元素恰好出現在每一行和每一列各一次。
反之，每個拉丁方都可以以多種方式成為一個擬群的乘法表。
態射
一個擬群或圈同態是兩個擬群（圈）之間的映射：f :Q →P 滿足f(xy) =f(x)f(y)。 擬群同態保持了左右除法以及單位元（如果有的話）。
例子
整數集合 Z 以及其上的減法 (−) 構成擬群（但不構成半群）。
所有非零的有理數的集合 Q* （或者所有非零實數構成的 R*）以及其上的除法 (÷) 構成一個擬群。
所有特徵不為2的域上的向量空間以及其上的二元運算x *y = (x +y) / 2 構成了一個冪等的交換的擬群。
每個斯坦納三元系統都定義了一個冪等交換的擬群：其運算為將a *b 對應到包含a 和b 的三元數組的第三個元。
非零八元數以及其上的乘法構成了一個圈，稱為Moufang圈.
一般來說，一個可除代數上的所有非零元構成一個擬群。
