基本介紹
圈擬陣是建立在圖G=(V，E)上的一類擬陣M(G)，其獨立集為不含圈的邊集E的子集，因此，圈擬陣的直觀形象十分鮮明，由於不同構的圖會有相同的圈擬陣，對圈擬陣的研究並不能取代圖的研究，它只能看做圖的一種延伸，對於圈擬陣M(G)，其圈正是圖G的圈，所以圈擬陣亦稱多邊形擬陣。
圖G的上圈是E的子集A，將A從G中移去以後會增加G的連通分支的數目，正如G的圈構成M(G)的圈一樣，以G的上圈為圈，對應地得到G上的另一類擬陣，稱為上圈擬陣，上圈擬陣亦稱鍵擬陣，圈擬陣和上圈擬陣互為對偶，且在任何域上均可表示，記上圈擬陣為M(G)。
相關性質
由於圈擬陣和上圈擬陣具有明顯的圖的特徵，所以藉助於同構的概念，可將它們延伸到其他一般擬陣，擬陣M=(E，I)，M=(E，I)同構，若且唯若在E和E之間有雙射φ，並保持獨立性，對於擬陣M，若有圖G存在，使得M與G的圈擬陣同構，則稱M是可圖的或稱M為圖擬陣.對應地，若M與G的上圈擬陣同構，則稱M是可上圖的，或稱M為上圖擬陣。例如，完全圖K，完全二部圖K的圈擬陣M(K)和M(K)是可圖的，但不是可上圖的。更一般地，G為平面圖，若且唯若它的圈擬陣M(G)是可上圖的.因此，擬陣的可圖性，本質上刻畫了圖的平面性。
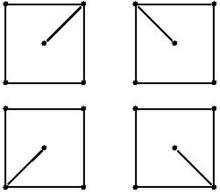圖1特別地，當G為歐拉圖時，它的邊集能劃分為圈，而在歐拉圖上建立的圈擬陣，稱為歐拉擬陣，更一般地，對於建立在集合E上的擬陣M，若E可以表示為M的互不重疊的圈的並集，則稱M為歐拉擬陣，若M的所有圈，其中元素的個數均為偶數時，則稱M為偶擬陣，二元擬陣為歐拉擬陣若且唯若其對偶是二元擬陣，作為一個既不是圖擬陣也不是上圖擬陣的例子，它就是旋擬陣，此擬陣由輪圖W=K+C產生，它的圈對應為C添加一條幅，例如，對於W，其圈如上圖 。
舉例
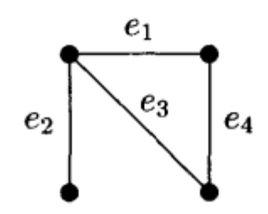
考慮圖G
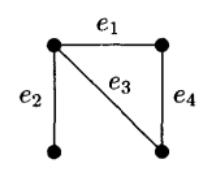圖2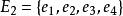
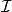圈擬陣
圈擬陣其邊集為 。我們要確定所有無圈子圖的邊集的集族 。由於每一個無圈子圖都是一個支撐樹的子圖，因此我們只要找出G的所有的支撐樹。不難看出G的全體支撐樹對應的邊子集是
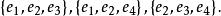圈擬陣因此，
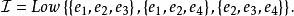圈擬陣