系統辨識實驗設計
正文
準則和限制 由參數估計理論得知：一切無偏估計量估計誤差的協方差矩陣總是以費歇信息矩陣M 的逆陣M-1為下界。而有效性估計的估計誤差協方差矩陣則達到了這個下界。估計誤差協方差矩陣是參數估計的精度標誌。在系統辨識中,費歇信息矩陣M 的元素通過數學模型顯式地或隱式地決定於系統的輸入ui和採樣間隔Δi等可控變數。因此由信息矩陣M 產生的標量函式J＝Φ(M),就可供作衡量不同實驗所包含信息的一種量度或準則。另外，在進行一項實驗時，實驗條件往往受到許多限制,例如：輸入信號的類型、輸入和輸出的振幅或功率、允許持續進行實驗的時間、最大和最小的採樣速度、採樣時間間隔（等間隔與不等間隔）等的限制。綜合最優實驗設計 當選定了一種實驗信息的量度準則之後,在某些約束條件下對輸入信號和採樣間隔(也可以包括預採樣濾波器)進行有約束的最最佳化計算,就可以得到在這個準則和約束條件下的綜合最優實驗設計。一般地說，綜合最優實驗設計很複雜，只有當模型具有簡單形式時，才能給出解析形式的條件，通常還要進行比較複雜的最最佳化計算才能得到結果。為了實用，常常採用次優設計。
單項最優實驗設計 除了綜合設計外，也可以考慮單項的最優輸入信號設計或單項的採樣間隔設計，這相對來說要簡單一些。在實際套用中，通過計算機進行採樣是等間隔的，因此最優輸入信號的設計問題成為系統辨識實驗設計中的主要內容。輸入信號因辨識的模型類的不同而異。例如模型類屬於頻率回響，則單頻正弦輸入信號常比方波信號為好；如果模型是帶有隨機噪聲的，則使用偽隨機信號比一般的方波信號好。輸入信號的設計有時域和頻域兩種途徑。
時域設計 輸入信號的時域設計是指設計結果為時域表示形式,即信號為時間t的函式。設系統具有線性傳遞形式：yt=G1(z)ut+G2(ε)t，其中{ut}和{yt}分別為輸入和輸出序列,{εt}是數學期望為0、協方差為
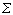的高斯白噪聲序列,G1和G2是傳遞函式,G2滿足條件: G2(∞)＝1。最優設計準則為關於輸入信號 ut的極小化目標函式J＝-log det嚔，其中嚔＝(1/N)M 為平均信息矩陣, N為信號序列的長度,M為費歇信息矩陣。為了不使輸入信號平均功率過大，造成系統的過分激勵，對輸入信號應加上功率限制：
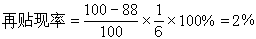。在這個約束條件下,使目標函式J對於時域輸入信號序列{ut}極小化,就能獲得時域的最優輸入信號{ut}。這是一個標準的非線性最優控制問題,原則上通過最最佳化計算可以求解,當G1(z)呏1，
時為滑動平均模型。這時問題有解析解,即滿足正交性條件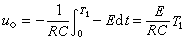 
頻域設計 輸入信號的頻域設計結果是求出信號中應包含各種頻率的成分及其振幅。如果信號長度N 允許足夠大，輸入信號{ut}可以用譜表示，對輸入信號的功率限制為
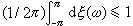，其中 ξ(ω)是輸入信號的功率譜，則頻域設計過程是對目標函式J=-log det嚔在上述功率約束條件下的最佳化過程。業已證明，總可以用有窮多個不同振幅的單頻正弦信號相加得到所要求的最優輸入信號。例如對於系統
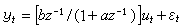，可以證明它的最優輸入信號是一單頻的正弦信號。