振盪間斷點屬於第二類間斷點。
毫無疑問,凡是間斷點x0,一定是f(x0)不存在(包括有定義不存在和無定義不存在)或者存在但不在函式上,即間斷點x0處的值一定是不存在或者存在且不同時等於該點處左右極限的值的。
一般在中國大陸教材中,間斷點x0處可以無定義,但在間斷點x0的去心鄰域內有定義,即間斷點雙側存在定義才會討論間斷點,沒有雙側定義不討論間斷,也就是你所學的基本上都不討論,也不考沒有雙側定義的間斷,這點要注意。但在國際教材中,比如菲氏《微積分教程》中,存在間斷點單側定義,即同一間斷點可以左側為無窮間斷,右側為跳躍間斷。
一般而言:
第一類間斷點:可去間斷點(間斷點處左右極限存在且相等),跳躍間斷點(間斷點處左右極限不相等)
第二類間斷點:凡是除去上述2個第一類間斷點以外,全部的間斷點都是第二類間斷點,包括但不僅限於無窮間斷點,振盪間斷點,單側定義間斷點等等。
四類間斷點區別:
左右極限存在且相等的間斷點,叫可去間斷點。
左右極限存在且不相等的間斷點,叫跳躍間斷點。
左右極限為無窮的間斷點,叫做無窮間斷點,其中無窮是個可以解出的答案,但一般視為極限不存在。
左右極限振盪不存在的間斷點,叫做振盪間斷點,其中振盪是不可以解出的答案,極限完全不存在。
振盪間斷點舉例說明:
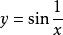 振盪間斷點
振盪間斷點函式在點x=0處沒有定義,且當x趨於0時,函式值在-1,1這兩個數之間交替振盪取值,極限不存在。