定義
間斷點及其分類
間斷點及其分類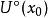
間斷點及其分類
間斷點及其分類 間斷點及其分類 間斷點及其分類 間斷點及其分類 間斷點及其分類設函式 在某 上有定義。若 在點 無定義，或 在點 有定義而不連續，則稱點 為函式 的間斷點或不連續點。
間斷點及其分類 間斷點及其分類若 為函式 的間斷點，則必出現下列情形之一：
間斷點及其分類 間斷點及其分類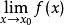
間斷點及其分類（i） 在點 無定義或極限 不存在；
間斷點及其分類 間斷點及其分類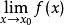 間斷點及其分類
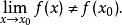間斷點及其分類（ii）） 在點 有定義且極限 存在，但
據此，我們對函式的間斷點作如下分類 ：
可去間斷點
若
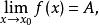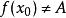間斷點及其分類 間斷點及其分類 間斷點及其分類
間斷點及其分類 間斷點及其分類 間斷點及其分類而 在點 無定義，或有定義但 ，則稱 為 的可去間斷點。
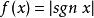間斷點及其分類
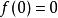間斷點及其分類例如，對於函式 ，因 ，而
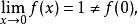間斷點及其分類
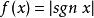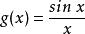間斷點及其分類 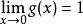間斷點及其分類
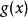間斷點及其分類
間斷點及其分類
間斷點及其分類 間斷點及其分類 間斷點及其分類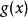 間斷點及其分類故 為 的可去間斷點。又如函式 ，由於 ，而 在 無定義，所以 是函式 的可去間斷點。
間斷點及其分類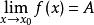 間斷點及其分類
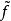間斷點及其分類
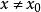間斷點及其分類
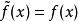間斷點及其分類
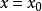間斷點及其分類
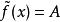間斷點及其分類
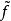間斷點及其分類 間斷點及其分類 間斷點及其分類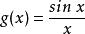 間斷點及其分類設 為函式 的可去間斷點，且 。我們按如下方法定義一個函式 ：當 時， ；當 時， 。易見，對於函式 ， 是它的連續點。例如，對上述的 ，我們定義
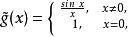間斷點及其分類
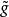間斷點及其分類 間斷點及其分類則 在 連續。
跳躍間斷點
間斷點及其分類 間斷點及其分類若函式 在點 的左、右極限都存在，但
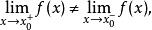間斷點及其分類 間斷點及其分類 間斷點及其分類則稱點 為函式 的跳躍間斷點。
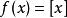間斷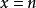點及其分類
間斷點及其分類
間斷點及其分類例如，對函式 ，當 （ 為整數）時有
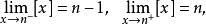間斷點及其分類 間斷點及其分類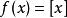 間斷點及其分類所以在整數點上函式 的左、右極限不相等，從而整數點都是函式 的跳躍間斷點。
可去間斷點和跳躍間斷點統稱為第一類間斷點。第一類間斷點的特點是函式在該點處的左、右極限都存在。
第二類間斷點
函式的所有其他形式的間斷點，即使得函式至少有一側極限不存在的那些點，稱為第二類間斷點。
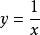間斷點及其分類
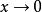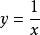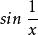間斷點及其分類 間斷點及其分類 間斷點及其分類
間斷點及其分類 間斷點及其分類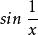 間斷點及其分類 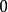間斷點及其分類
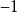間斷點及其分類
間斷點及其分類
間斷點及其分類例如，函式 當 不存在有限的極限，故 是 的第二類間斷點。函式 在點 處的左、右極限都不存在，故 是 的第二類間斷點。當趨近於 時，函式在 和 之間取值，這樣的間斷點稱為振盪間斷點。
無窮間斷點和振盪間斷點都屬於第二類間斷點。
便於理解和記憶，間斷點的分類概括如下：
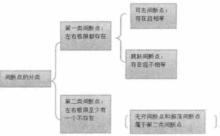間斷點分類概括圖幾個有間斷點的函式
（1）狄利克雷函式
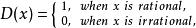間斷點及其分類
間斷點及其分類
間斷點及其分類在定義域 上每一點 都是第二類間斷點。
（2）函式
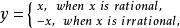間斷點及其分類 間斷點及其分類
間斷點及其分類僅在點 連續， 時是第二類間斷點。
（3）整數部函式
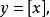間斷點及其分類與小數部函式
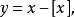間斷點及其分類 間斷點及其分類都是在 為整數時是第一類不可去間斷點，在這些點仍是右連續的。
（4）黎曼函式
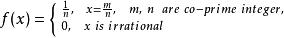間斷點及其分類在每一個無理點都連續，而在異與零的有理點都不連續。
（5）函式
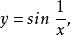間斷點及其分類 間斷點及其分類 間斷點及其分類在點 附近函式振盪而無極限， 是它的第二類間斷點。
（6）函式
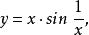間斷點及其分類 間斷點及其分類在點 是可去間斷點，並且
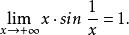間斷點及其分類（7）函式
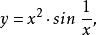間斷點及其分類 間斷點及其分類（8）函式
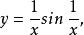間斷點及其分類 間斷點及其分類在點 是第二類間斷點。
套用
例 求分段函式
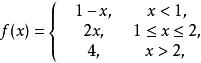間斷點及其分類的間斷點並判斷其類型。
解 因為
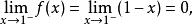間斷點及其分類
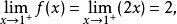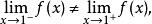間斷點及其分類
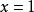間斷點及其分類
間斷點及其分類 間斷點及其分類所以， 是 的跳躍間斷點。
又因為
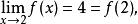間斷點及其分類 間斷點及其分類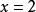
間斷點及其分類所以在處連續。
