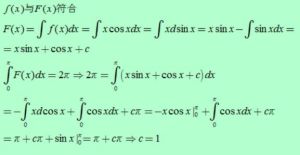基本內容
原函式存在定理為:若f(x)在[a,b]上連續,則必存在原函式。
此條件為充分條件,而非必要條件。即若f(x)存在原函式,不能推出f(x)在[a,b]上連續。
設F'(x)=f(x),f(x)在x=x0處不連續,則x0必為第二類間斷點中的振盪間斷點或者無窮間斷點(有例子),而非第一類間斷點。
當f(x)存在第二類間斷點時,不能確定是否存在原函式,這種情況下結論與f(x)的表達式有關【參考2013數一全書P95 例3.41】【參考2014數一全書P100 例3.37 例3.38】
原函式存在的三個結論:
如果f(x)連續,則一定存在原函式
如果f(x)不連續,但有第二類間斷點,那么就有可能存在原函式
如果f(x)不連續,並存在第一類間斷點,那就一定不存在原函式