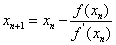數值計算方式
手動開立方
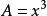 手動開方
手動開方設, ,求X.稱為開立方。 開立方有一個用於數值計算的公式:
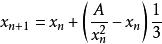 手動開方
手動開方例如,A=5,即求
5介於1的3次方;至2的3次方;之間(1的3次方=1,2的3次方=8)
初始值X0可以取1.1,1.2,1.3,1.4,1.5,1.6,1.7,1.8,1.9,都可以。例如我們取X0 = 1.9按照公式:
第一步:X1=1.9+(5/1.9^2;-1.9)1/3=1.7。
即5/1.9×1.9=1.3850416,1.3850416-1.9=-0.5149584,-0.5149584×1/3=-0.1716528,1.9+(-0.1716528)=1.7。即取2位數值,,即1.7。
第二步:X2=1.7+(5/1.7^2;-1.7)1/3=1.71。
即5/1.7×1.7=1.73010,1.73-1.7=0.03,0.03×1/3=0.01,1.7+0.01=1.71。取3位數,比前面多取一位數。
第三步:X3=1.71+(5/1.71^2;-1.71)1/3=1.709.
第四步:X4=1.709+(5/1.709^2;-1.709)1/3=1.7099
這種方法可以自動調節,第一步與第三步取值偏大,但是計算出來以後輸出值會自動轉小;第二步,第四步輸入值
偏小,輸出值自動轉大。即5=1.7099^3;
當然初始值X0也可以取1.1,1.2,1.3,。。。1.8,1.9中的任何一個,都是X1 = 1.7 > 。當然,我們在實際中初始值最好採用中間值,即1.5。 1.5+(5/1.5^2;-1.5)1/3=1.7。
手動開平方
如果用這個公式開平方,只需將3改成2,2改成1。即:
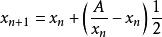 手動開方
手動開方例如,A=5:
5介於2的平方至3的平方;之間。我們取初始值2.1,2.2,2.3,2.4,2.5,2.6,2.7,2.8,2.9都可以,我們最好取 中間值2.5。 第一步:2.5+(5/2.5-2.5)1/2=2.2;
即5/2.5=2,2-2.5=-0.5,-0.5×1/2=-0.25,2.5+(-0.25)=2.25,取2位數2.2。
第二步:2.2+(5/2.2-2.2)1/2=2.23;
即5/2.2=2.272,2.272-2.2=-0.072,-0.072×1/2=-0.036,2.2+0.036=2.23。取3位數。
第三步:2.23+(5/2.23-2.23)1/2=2.236。
即5/2.23=2.242,2.242-2.23=0.012,0.012×1/2=0.006,2.23+0.006=2.236.
每一步多取一位數。這個方法又叫反饋開方,即使你輸入一個錯誤的數值,也沒有關係,輸出值會自動調節,接近準確值。當輸入值與輸出值一樣,那麼就是精確值。例如:
A=94249:94249介入300平方---400平方之間。初始值可以取310,320,330,340,350,360,370,380,390.我們取中間值350為初始值。
350+(94249/350-350)1/2=310.
310+(94249/310-310)1/2=307
307+(94249/307-307)1/2=307.
即94249=307^2
算法基礎
本段的算法源於數值計算里的牛頓疊代法或切線法,即:
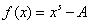 手動開方
手動開方,其中的指數s是2或3或其他任意的整數。
九章算術
手動開平方
算法為:
1.將被開方數的整數部分從個位起向左每隔兩位劃為一段,用撇號分開,分成幾段,表示所求平方根是幾位數;小數部分從最高位向後兩位一段隔開,段數以需要的精度+1為準。
2.根據左邊第一段里的數,求得平方根的最高位上的數。(在右邊例題中,比5小的平方數是4,所以平方根的最高位為2。)
3.從第一段的數減去最高位上數的平方,在它們的差的右邊寫上第二段數組成第一個餘數。
4.把第二步求得的最高位的數乘以20去試除第一個餘數,所得的最大整數作為試商。(右例中的試商即為[152/(2×20)]=[3.8]=3。)
5.用第二步求得的的最高位數的20倍加上這個試商再乘以試商。如果所得的積小於或等於餘數,試商就是平方根的第二位數;如果所得的積大於餘數,就把試商減小再試,得到的第一個小於餘數的試商作為平方根的第二個數。(即3為平方根的第二位。)
6.用同樣的方法,繼續求平方根的其他各位上的數。用上一個餘數減去上法中所求的積(即152-129=23),與第三段數組成新的餘數(即2325)。這時再求試商,要用前面所得到的平方根的前兩位數(即23)乘以20去試除新的餘數(2325),所得的最大整數為新的試商。(2325/(23×20)的整數部分為5。)
7.對新試商的檢驗如前法。(右例中最後的餘數為0,剛好開盡,則235為所求的平方根。)
如遇開不盡的情況,可根據所要求的精確度求出它的近似值。在《九章算術》里就已經介紹了上述筆算開平方法。
以《九章算術》中求55225的開方為例。
實例及對應算法說明:
①將被開方數的整數部分從個位起向左每隔兩位劃為一段,用撇號分開,分成幾段,表示所求平方根是幾位數;小數部分從最高位向後兩位一段隔開,段數以需要的精度+1為準。
5’ 52’ 25
②根據左邊第一段里的數(5),求得平方根的最高位上的數(2)。
2----------------------------------------(平方根)
③從第一段的數減去最高位上數的平方,在它們的差的右邊寫上第二段數組成第一個餘數。
5’ 52’ 25
4
1’ 52 -----------------------------------(第一個餘數)
④把第二步求得的最高位的數乘以20去試除第一個餘數,所得的最大整數作為試商。(152為被除數,平方根乘以20為除數,得到商及相關餘數)
152/(2×20)=3+相關餘數-----------(3為試商)
⑤用第二步求得的的最高位數的20倍加上這個試商再乘以試商。如果所得的積小於或等於餘數,試商就是平方根的第二位數;如果所得的積大於餘數,就把試商減小再試,得到的第一個小於餘數的試商作為平方根的第二個數。(即3為平方根的第二位。)
(2×20+3)×3=129------------------( 用第二步求得的的最高位數(即已得的平方根,此處為2)的20倍加上試商(此處為3)再乘以試商)
比較1‘52(餘數)與1'29(比較數)大小,如果比較數小於等於餘數,則試商有效,否則,試商減1,再比較。
到此,平方根的第一位2,第二位3確認。
⑥用同樣的方法,繼續求平方根的其他各位上的數。用上一個餘數減去上法中所求的積(即152-129=23),與第三段數組成新的餘數(即2325)。這時再求試商,要用前面所得到的平方根的前兩位數(即23)乘以20去試除新的餘數(2325),所得的最大整數為新的試商。(2325/(23×20)的整數部分為5。)
23’ 25---------------------------------(新的餘數)
2325/(23×20)=5+相關餘數--------(5為第三位數的試商)
(23×20+5)×5=2325 ----------------(已得的平方根,此處為23)的20倍加上相應位試商(此處為5)再乘以相應位試商)
比較23’ 25 (新的餘數)與23’ 25(比較數)之間的大小,規則同上。(如果比較數小於等於餘數,則試商有效,否則,試商減1,再比較。)
0 ----------------------------------------(得到0或者相應的精度為止)
於是,235即為所求。
圖解為:
|5’ 52’ 25 (1)
2 ----------------------------------------平方根第一位
|5’ 52’ 25 (2)
|4
|1’ 52 (3) ------------------------------------第一個餘數
152/(2×20)=3+... ---------- 第一個試商
|1’ 52’ (4)
(2×20+3)×3=129 ----------第一個比較數
|1 52 (5)
1 29
| 23’ 25 (6) -----------------------------新的餘數
2325/(23×20)=5+... ----- 新的試商
| 23’ 25 (7)
(23×20+5)×5=2325------ 新的比較數
0 (8)------------------------------------------------比較結果
《九章算術》少廣章:
第十二題:今有積五萬五千二百二十五步。問為方幾何?
答曰:二百三十五步。
開方術曰:
置積為實。借一算。步之。超一等。議所得。以一乘所借一算為法。而以除。除已。倍法為定法。其復除。折法而下。復置借算步之如初。以複議一乘之。所得副。以加定法。以除。以所得副從定法。復除折下如前。
若開之不盡者為不可開,當以面命之。若實有分者,通分內子為定實。乃開之,訖,開其母報除。若母不可開者,又以母乘定實,乃開之,訖,令如母而一。
手動開立方
1.將被開立方數的整數部分從個位起向左每三位分為一組;
2.根據最左邊一組,求得立方根的最高位數;
3.用第一組數減去立方根最高位數的立方,在其右邊寫上第二組數;
4.用求得的最高位數的平方的300倍試除上述餘數,得出試商;
5.把求得的最高位數的平方的300倍與試商的積、求得的最高位數的30倍與試商的平方的積和試商的立方寫在豎式左邊,觀察其和是否大於餘數,若大於,就減小試商再試,若不大於,試商就是立方根的第二位數;
6.用同樣的方法,繼續求立方根的其他各位上的數。對新試商的檢驗亦如前法。
此開立方方法主要參考:
未知作者名號。在另外一個網頁中有署名“陳梓瀚”者,不知是否同一作者。本文中有改動。
以《九章算術》中求1860867立方根為例,圖解說明。
| 1’ 860’ 867 (1)
1 | 1’ 860’ 867 (2)
| 1
| 860 (3)
860/(12×300)=2+... | 860 (4)
1[2]×300×2=600 |
1×30×2[2]=120 |
2[3]=8 | 860 (5)
600+120+8=728
| 132’ 867 (6)
132867/(12[2]×300)=3+... | 132’ 867 (7)
12[2]×300×3=12600 |
12×30×3[2]=3240 |
3[3]=27 | 132’ 867 (8)
12600+3240+27=132’ 867
| 0 (9)
0 (10)
於是,123即為所求。
《九章算術》少廣章:
第一九題:今有積一百八十六萬八百六十七尺。問為立方幾何?
答曰:一百二十三尺。
開立方術曰:
置積為實。借一算步之,超二等。議所得,以再乘所借一算為法 ,而除之。除已,三之為定法。復除,折而下。以三乘所得數置中行。復借一算置下行。步之 ,中超一,下超二等。復置議,以一乘中,再乘下,皆副以加定法。以定法除。除已,倍下、 並中從定法。復除,折下如前。
開之不盡者,亦為不可開。若積有分者,通分內子為定實。定 實乃開之,訖,開其母以報除。若母不可開者,又以母再乘定實,乃開之。訖,令如母而一。