代數函式

非超越函式則稱為代數函式。代數函式的例子包括多項式和平方根函式。一函式的不定積分運算是超越函式的豐富來源，如對數函式便來自倒數函式的不定積分。在微分代數裡，人們研究不定積分如何產生與某類“標準”函式代數獨立的函式，例如將三角函式與多項式的合成取不定積分。

正文

由不可約方程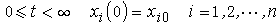

(1)

確定的多值函式,式中αj(z)(j=0,1,…,n)是z的多項式。由(1)式和下列方程

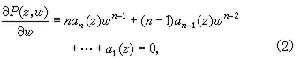
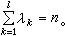消去w得到的判別式 D（z）是z的非恆為零的多項式。若z0不是D（z）的零點，則p(z0,w)＝0恰有n個判別的根wj（j＝1，2，…，n）。若再設z0不是αn（z）之零點，則由隱函式定理知，存在 n個判別的正則函數元素（wj(z)，B(z0)）（j＝1，2，…，n）屬於方程（1），即在以z0為心的某個圓B(z0)內滿足 P（z,wj(z)）＝0，且wj（z0）＝wj(j＝1，2，…，n)。若 z0是D(z)之零點，則 P（z0,w）＝0 有重根 wk, 設其重級為λk, 且 此時在z0點穿洞的小圓妋(z0)上n個函式元素能分為l個循環 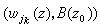(jk=1，2，…，λk,k=1,2,…,l)並且當沿著在妋(z0)中的曲線圍繞z0開拓時,同一循環中的函式元素互相置換。設由 w1(z)在妋(z0)中開拓所得之多值函式為wλ(z),則它可表為某個圓B(z0)內收斂的分數冪級數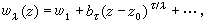此時（wλ(z)，B(z0)），是屬於方程 (1) 的代數函式元素。當 z0=時，以ζ=1/z代之，若w1=，則以u=1/w 代之。再者由屬於不可約方程(1)的任一函式元素(正則的或代數的)出發可以用解析開拓方法來聯接整個函式,即屬於方程 (1)的函式元素經解析開拓所得的函式元素仍屬於方程(1)，並且任兩個屬於方程(1)的函式元素能經解析開拓互相得到。因此代數函式是在擴充的複平面╦＝C ∪{}上僅具有有限多個代數分支點和極點的完全解析函式。反之，具有上述特徵的完全解析函式，且對於一固定點z0,僅具有有限個以z0為中心的函式元素者,滿足一不可約代數方程,且除去一個非零的常數因子外,此方程是惟一的。
套用 B.黎曼的方法可以構造一個新的曲面以代替z平面，使得在此曲面上代數函式為通常的單值函式，這個曲面即是黎曼曲面。相應於代數函式的黎曼曲面是緊的，曲面的虧格即定義為代數函式的虧格。例如，超橢圓曲線 w2=P(z)的虧格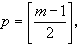其中P(z)是z的m 次多項式，【α】表示α的整數部分。
由方程(1)聯繫著的z和w 的有理函式R(z，w)之積分稱為阿貝爾積分。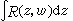對於這個積分有一系列標準形式，使得任一這類型的積分能通過適當的變數變換變為其中一個標準形式。這個積分是一多值函式，其多值性不僅產生於R 的留數和 w(z)的多值性,而且還依賴於相應的黎曼曲面的拓撲性質。
關於阿貝爾積分之研究還導致代數函式的單值化的可能性問題。代數函式單值化問題是對於方程 (1)所確定的 z和w 的多值對應關係 z凮w，去尋找一個參數表示(z(t)，w(t))，其中z(t)和 w(t)是定義於╦ 的子域T上的t的單值函式。代數函式的單值化問題引起了一般單值化理論之發展。19世紀下半葉和20世紀的最初10年，世界上許多傑出的數學家，如黎曼、F.克萊因、H.龐加萊、H.A.施瓦茲、B.H.紐曼和P.克貝等人都作出了重要的貢獻，最後於1908年由克貝和龐加萊同時解決。代數函式這個特殊情形的解決，曾引起拓撲學與共形映射理論之結合。對於代數函式單值化的基本結論是:虧格p=0的代數函式由有理函式單值化，即 (z(t)，w(t))是兩個t的有理函式；虧格p=1時, 由雙周期橢圓函式單值化；虧格p≥2時，由單位圓內對某個富克斯群自守的亞純函式單值化。
代數函式論還沿著算術的方向和幾何的方向發展，後者是用幾何方法研究代數曲線，並發展為代數幾何。

參考書目

　P. Appell et E.Goursat,Théorie des Fonctions Algébrique de Leurs Intégralés,T.1～2,Gauthier-Villars,Paris,1929～1930.
　R. Nevanlinna,Uniformisierung, Springer-Verlag, Berlin,1953.