簡介
有理根定理是一個關於任意整係數方程的有理根的定理。
 有理根定理
有理根定理在代數中,有理根定理(或有理根測試,有理零定理,有理零測試或定理)表示對多項式方程的有理解與整數係數的約束。
 有理根定理
有理根定理這些解是方程左側多項式的可能d 根(相當於零)。
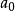 有理根定理
有理根定理 有理根定理
有理根定理 有理根定理
有理根定理如果和不為零,那么當最低項(即p和q的最大公約數為1)寫為的分數時,每個有理解x滿足
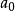 有理根定理
有理根定理 有理根定理
有理根定理p是常數項的整數因子,q是導數係數的整數因子。
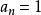 有理根定理
有理根定理有理根定理是高斯引理對多項式因式分解的特殊情況(單線性因子)。 如果導數係數,則整數根定理是有理根定理的特殊情況。
套用
為了確定一個多項式是否有任何有理根,使用該定理,如果是這樣就可以找出它們。 由於定理給出了完全減少的有理根的分子和分母作為某些數的除數的約束,所以可以檢查除數的所有可能的組合,或者找出合理的根,或者確定沒有一個。 如果找到一個或多個,則可以將它們從多項式中分解出來,導致較低程度的多項式,其根也是原始多項式的根。
立方公式
一般三次方程:
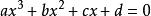 有理根定理
有理根定理 有理根定理
有理根定理整數係數在複平面中具有三個解。 如果通過有理根定理髮現沒有合理的解,則代數方法表達解的唯一方法是使用立方根。 但是如果測試找到三個合理的解,那么可以避免立方根。 並且如果發現存在一個合理的解r,則可以使用多項式長分割從三次多項式中求出,得到二次多項式,其中兩根是立方的剩餘兩根;並且這些可以使用二次公式找到,再次避免使用立方根。
證明
 有理根定理
有理根定理對於一些a0,...,an∈Z,令
 有理根定理
有理根定理並且假設對於一些互質p、q,,q∈Z則
 有理根定理
有理根定理如果我們兩邊都乘以q,將常數項轉換到右邊,並將左側的p代入,得到
 有理根定理
有理根定理 有理根定理
有理根定理 有理根定理
有理根定理我們看到p乘以圓括弧中的整數等於,所以p除以 。
如果我們把它轉移到右邊,並把左邊的q值換算出來,我們就得到了,
 有理根定理
有理根定理使用高斯引理證明:
 有理根定理
有理根定理 有理根定理
有理根定理 有理根定理
有理根定理 有理根定理
有理根定理 有理根定理
有理根定理 有理根定理
有理根定理 有理根定理
有理根定理如果存在分解多項式的所有係數的非平凡因子,則可以除以係數的最大公因數,以便獲得高斯引理意義上的原始多項式; 這不會改變一套理性根源,只能加強可分割條件。 這個引理說,如果中的多項式因子,那么它也將作為原始多項式的乘積。 現在任何合理的根對應於多項式的中的1的因子,並且其原始代表是,假設p和q是互質的。 但是,的中的任何多項式都可以被q整除,並且可以被p整除的常數項可以被引導。 這個論點表明,更普遍地說,P的任何不可約因子都可以被認為具有整數係數,並且前導和常數係數除以P的相應係數。
舉例
第一個
在多項式中
 有理根定理
有理根定理任何合理根完全減少將必須有一個分子均勻分為1和一個分母均勻分為2因此唯一可能的合理根是±1/2和±1; 由於這些都不等於多項式為零,所以沒有合理的根。
第二個
在多項式中
 有理根定理
有理根定理唯一可能的合理根將有分子6和分母1的分母,將可能性限制在±1,±2,±3和±6。 其中,1,2和-3將多項式等效為零,因此是其合理根。
第三個
下式多項式的根
 有理根定理
有理根定理一定在符號下面表示的數字之中,
 有理根定理
有理根定理其中列出了8個可能的答案:
 有理根定理
有理根定理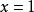 有理根定理
有理根定理 有理根定理
有理根定理 有理根定理
有理根定理 有理根定理
有理根定理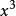 有理根定理
有理根定理這些根可以使用霍納的方法進行測試。 在這種特殊情況下,只有一個合理根。 如果根候選不使多項式等於零,則可用於縮短剩餘候選列表。例如,不起作用,因為多項式然後等於1。這意味著用代入中的常數項1,而係數保持與的係數相同的多項式。 因此,套用有理根定理可以產生以下可能的根t:
 有理根定理
有理根定理因此,
 有理根定理
有理根定理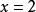 有理根定理
有理根定理 有理根定理
有理根定理排除在兩個列表上都不出現的根本的候選人。 理性根本候選人名單因此縮小到和。
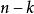 有理根定理
有理根定理 有理根定理
有理根定理如果找到k個理性根(k≥1),霍納方法也將產生一個度數的多項式,其根與理性根恰好是原始多項式的根。 也許沒有一個候選人是解決方案的情況; 在這種情況下,等式設定多項式的方程式沒有理性的解。 如果方程缺少常數項,則0是方程的有理解之一。
