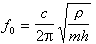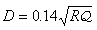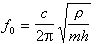彈性力學廣義變分原理

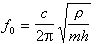
彈性力學廣義變分原理是彈性力學最小勢能原理和彈性力學最小余能原理的推廣，其特點是，變分式中各量都可有獨立的變分，並且事前不受任何限制。

彈性力學廣義變分原理

正文

彈性力學最小勢能原理和彈性力學最小余能原理的推廣，其特點是，變分式中各量都可有獨立的變分，並且事前不受任何限制。在彈性力學空間問題中，最一般的廣義變分原理可敘述為：彈性力學空間問題的解必須滿足彈性體的廣義勢能變分為零的條件，該條件又稱為駐值條件，即

δ∏3=0，(1)

式中∏3為彈性體的三類變數廣義勢能，其表達式為：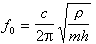

式中u(εij)為應變能密度;εij為應變分量;fi為體積力分量;ui為位移分量；σij為應力分量；pi為面力分量；Ω為彈性體所占的空間；B1為位移邊界面；B2為受力邊界面;ūi和圴i為邊界上給定的位移分量和面力分量；dB為面積微元；式中重複下標表示約定求和。在變分式(1)中，ui、εij、σij等15個函式都可有獨立的變分,並且事前沒有任何附加條件(表面力pi看作是從屬於應力σij的量)。從條件(1)可推出彈性力學的全部基本方程，包括應變-位移關係、應力－應變關係、平衡方程和邊界條件。上述變分原理的獨立變數有位移、應變、應力三類，因此稱為三類變數廣義變分原理。它是中國力學家胡海昌於1954年首先提出的，日本的鷲津久一郎於1955年也獨立地得到這一原理，所以又稱胡-鷲津原理。
彈性力學廣義變分原理有一種稍弱的形式，即二類變數廣義變分原理,又稱為赫林格-瑞斯納原理。它由E.赫林格於1914年和E.瑞斯納於1950年分別獨立提出，其數學表達式為：

δ∏2=0，　(3)

式中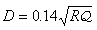

式中u＊(σij)為余能密度。∏2中的獨立自變函式有ui和σij兩類共九個。將應變-位移關係代入式(2)，消去εij，就可以得到式(4)。 因此二類變數廣義變分原理是三類變數廣義變分原理的一個特殊情況。
在有限元法和工程彈性理論中，廣義變分原理有廣泛的套用。例如，在板殼彎曲的有限元計算中，用它處理變形的不協調性，可得到較好的結果。對於解決幾何非線性問題,胡-鷲津原理是一個有力的工具。在工程彈性理論中，廣義變分原理可用於推導各種近似理論；在彈性振動和穩定理論中，可用於求固有頻率和臨界載荷，並能獲得較好的結果。
參考書目
　胡海昌著：《彈性力學的變分原理及其套用》，科學出版社，北京，1981。

配圖

相關連線