應力函式
最有名的應力函式是彈性力學平面問題中的艾里應力函式。如果沒有體力，平面中的三個應力分量σxx、σyy、τxy滿足下列方程：
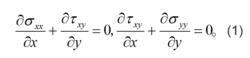應力函式和位移函式根據方程(1),可將應力分量用一個函式φ（x，y）表示為：
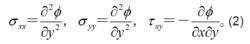應力函式和位移函式φ便是艾里應力函式。對於均勻和各向同性的物體,φ是一個雙調和函式，即它滿足下列雙調和方程：
ΔΔφ=0， (3)
式中Δ是平面的拉普拉斯算符。引入φ後,平面問題原來的8個未知函式(兩個位移分量、三個應變分量和三個應力分量σxx、σyy、τxy就歸結為一個函式φ。這對求解具體問題很有好處。
在彈性柱體的扭轉問題中,剪應力分量τxz、τyz滿足下列平衡方程：
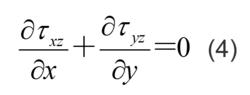應力函式和位移函式據此可將τxz、τyz用一個函式Ψ(x，y)表示為：
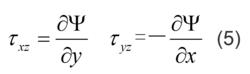應力函式和位移函式Ψ稱為普朗特應力函式。對於均勻和各向同性的柱體,Ψ滿足下列方程：
ΔΨ=-2Gθ， (6)
式中G為材料的剪下模量（見材料的力學性能）;θ為單位長度的扭轉角。
位移函式
在求解彈性力學的空間問題時，也可以用六個應力函式代替原來的六個應力分量，但好處不多。所以，一般多採用各種位移函式。對於均勻和各向同性彈性體，位移分量u1、u2、u3滿足下列平衡方程：
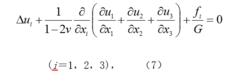應力函式和位移函式式中Δ是空間中的拉普拉斯算符；ν為材料的泊松比；G為剪下模量；fi為體力分量。方程(7)的解可以表達成多種形式。一種形式為：
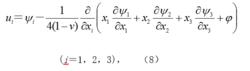應力函式和位移函式
應力函式和位移函式式中ψ1、ψ2、ψ3、 四個函式滿足下列方程：
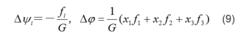應力函式和位移函式 應力函式和位移函式函式ψ1、ψ2、ψ3、
稱為布森涅斯克-帕普科維奇-紐勃位移函式。 彈性力學中許多空間問題的解都是從公式(8)推導出來的。方程(7)還有另一種形式的解，即
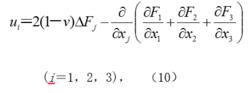應力函式和位移函式式中Fi滿足下列方程：
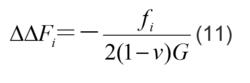應力函式和位移函式函式F1、F2、F3稱為布森涅斯克-索米利亞納－伽遼金位移函式。對於迴轉體的軸對稱問題，公式(10)可作許多簡化。取對稱軸為z軸(x3軸),記r為所考慮點到z軸的距離,並記位移在r、z軸上的投影分別為u、w。若┃1=┃2=0，可取F1=F2=0，F3=F(r，z)。這樣由公式(10)可得到：
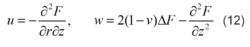應力函式和位移函式式中,即柱坐標中的拉普拉斯算符；F滿足下列方程：
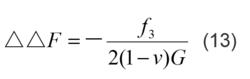應力函式和位移函式公式(12)中的函式F稱為樂甫位移函式。 在求解軸對稱問題時，經常利用公式(12)。
在f1=f2=0的情況下,即使不是軸對稱問題,方程(7)的解也可用一組位移函式F、f表示如下：
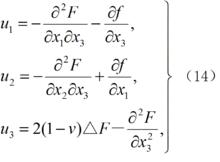應力函式和位移函式式中F、f滿足下列方程：
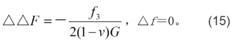應力函式和位移函式這組位移函式特別適用於求解無限體、半無限體和厚板等問題。
