簡介
 彈性力學
彈性力學彈性力學是固體力學的重要分支,它研究彈性物體在外力和其它外界因素作用下產生的變形和內力,也稱為彈性理論。它是材料力學、結構力學、塑性力學和某些交叉學科的基礎,廣泛套用於建築、機械、化工、航天等工程領域。彈性體是變形體的一種,它的特徵為:在外力作用下物體變形,當外力不超過某一限度時,除去外力後物體即恢復原狀。絕對彈性體是不存在的。物體在外力除去後的殘餘變形很小時,一般就把它當作彈性體處理。
發展簡史
彈性力學的發展大體分為四個時期。
人類從很早時就已經知道利用物體的彈性性質了,比如古代弓箭就是利用物體彈性的例子。當時人們還是不自覺的運用彈性原理,而人們有系統、定量地研究彈性力學,是從17世紀開始的。
 彈性力學
彈性力學發展初期的工作是通過實踐,探索彈性力學的基本規律。這個時期的主要成就是R.胡克於1678年發表的彈性體的變形與外力成正比的定律,後來被稱為胡克定律。第二個時期是理論基礎的建立時期。這個時期的主要成就是,從1822~1828年間,在A.-L·柯西發表的一系列論文中明確地提出了應變、應變分量、應力和應力分量概念,建立了彈性力學的幾何方程、平衡(運動)微分方程,各向同性和各向異性材料的廣義胡克定律,從而為彈性力學奠定了理論基礎。
彈性力學的發展初期主要是通過實踐,尤其是通過實驗來探索彈性力學的基本規律。英國的胡克和法國的馬略特於1680年分別獨立地提出了彈性體的變形和所受外力成正比的定律,後被稱為胡克定律。牛頓於1687年確立了力學三定律。
同時,數學的發展,使得建立彈性力學數學理論的條件已大體具備,從而推動彈性力學進入第二個時期。在這個階段除實驗外,人們還用最粗糙的、不完備的理論來處理一些簡單構件的力學問題。這些理論在後來都被指出有或多或少的缺點,有些甚至是完全錯誤的。
在17世紀末第二個時期開始時,人們主要研究梁的理論。到19世紀20年代法國的納維和柯西才基本上建立了彈性力學的數學理論。柯西在1822~1828年間發表的一系列論文中,明確地提出了應變、應變分量、應力和應力分量的概念,建立了彈性力學的幾何方程、運動(平衡)方程、各向同性以及各向異性材料的廣義胡克定律,從而奠定了彈性力學的理論基礎,打開了彈性力學向縱深發展的突破口。
第三個時期是線性各向同性彈性力學大發展的時期。這一時期的主要標誌是彈性力學廣泛套用於解決工程問題。同時在理論方面建立了許多重要的定理或原理,並提出了許多有效的計算方法。
 物理學家H·R·赫茲解決了接觸問題
物理學家H·R·赫茲解決了接觸問題1855~1858年間法國的聖維南發表了關於柱體扭轉和彎曲的論文,可以說是第三個時期的開始。在他的論文中,理論結果和實驗結果密切吻合,為彈性力學的正確性提供了有力的證據;1881年德國的赫茲解出了兩彈性體局部接觸時彈性體內的應力分布;1898年德國的基爾施在計算圓孔附近的應力分布時,發現了應力集中。這些成就解釋了過去無法解釋的實驗現象,在提高機械、結構等零件的設計水平方面起了重要作用,使彈性力學得到工程界的重視。
在這個時期,彈性力學的一般理論也有很大的發展。一方面建立了各種關於能量的定理(原理)。另一方面發展了許多有效的近似計算、數值計算和其他計算方法,如著名的瑞利——里茲法,為直接求解泛函極值問題開闢了道路,推動了力學、物理、工程中近似計算的蓬勃發展。
從20世紀20年代起,彈性力學在發展經典理論的同時,廣泛地探討了許多複雜的問題,出現了許多邊緣分支:各向異性和非均勻體的理論,非線性板殼理論和非線性彈性力學,考慮溫度影響的熱彈性力學,研究固體同氣體和液體相互作用的氣動彈性力學和水彈性理論以及粘彈性理論等。磁彈性和微結構彈性理論也開始建立起來。此外,還建立了彈性力學廣義變分原理。這些新領域的發展,豐富了彈性力學的內容,促進了有關工程技術的發展。
基本內容
彈性力學所依據的基本規律有三個:變形連續規律、應力-應變關係和運動(或平衡)規律,它們有時被稱為彈性力學三大基本規律。彈性力學中許多定理、公式和結論等,都可以從三大基本規律推導出來。
連續變形規律是指彈性力學在考慮物體的變形時,只考慮經過連續變形後仍為連續的物體,如果物體中本來就有裂紋,則只考慮裂紋不擴展的情況。這裡主要使用數學中的幾何方程和位移邊界條件等方面的知識。
 相關書籍
相關書籍求解一個彈性力學問題,就是設法確定彈性體中各點的位移、應變和應力共15個函式。從理論上講,只有15個函式全部確定後,問題才算解決。但在各種實際問題中,起主要作用的常常只是其中的幾個函式,有時甚至只是物體的某些部位的某幾個函式。所以常常用實驗和數學相結合的方法,就可求解。
數學彈性力學的典型問題主要有一般性理論、柱體扭轉和彎曲、平面問題、變截面軸扭轉,迴轉體軸對稱變形等方面。
在近代,經典的彈性理論得到了新的發展。例如,把切應力的成對性發展為極性物質彈性力學;把協調方程(保證物體變形後連續,各應變分量必須滿足的關係)發展為非協調彈性力學;推廣胡克定律,除機械運動本身外,還考慮其他運動形式和各種材科的物理方程稱為本構方程。對於彈性體的某一點的本構方程,除考慮該點本身外還要考慮彈性體其他點對該點的影響,發展為非局部彈性力學等。
基本規律
彈性力學所依據的基本規律有三個:變形連續規律、應力-應變關係和運動(或平衡)規律,它們有時被稱為彈性力學三大基本規律。彈性力學中許多定理、公式和結論等,都可以從三大基本規律推導出來。
①變形連續規律 彈性力學(和剛體的力學理論不同)考慮到物體的變形,但只限於考慮原來連續、變形後仍為連續的物體,在變形過程中,物體不產生新的不連續面。如果物體中本來就有裂紋,則彈性力學只考慮裂紋不擴展的情況。
反映變形連續規律的數學方程有兩類:幾何方程和位移邊界條件。幾何方程反映應變和位移的聯繫,它的力學含義是,應變完全由連續的位移所引起,在笛卡兒坐標系中,幾何方程為:
![彈性力學[固體力學的重要分支]](/img/6/34e/wZwpmL2YTMxEDN3kDN2QTN1UTM1QDN5MjM5ADMwAjMwUzL5QzL0EzLt92YucmbvRWdo5Cd0FmLxE2LvoDc0RHa.jpg) 彈性力學[固體力學的重要分支]
彈性力學[固體力學的重要分支]式中 x為坐標系的坐標; u為與 x相應的位移分量;為應變分量。
若所考慮的物體 Q在其一部分邊界 B上和另一物體 Q相連線,而且 Q在 B上的位移為已知量,在 B上便有位移邊界條件
![彈性力學[固體力學的重要分支]](/img/d/bd5/wZwpmL4ATO0ATM1ATN2QTN1UTM1QDN5MjM5ADMwAjMwUzLwUzL3UzLt92YucmbvRWdo5Cd0FmL0E2LvoDc0RHa.jpg) 彈性力學[固體力學的重要分支]
彈性力學[固體力學的重要分支]式中 u是 Q的位移。式(2)表示 Q和 Q兩物體在 B上貼合緊密,沒有間隙。反之則表示有間隙,違反了變形後繼續保持連續的基本要求。
②應力-應變關係 彈性體中一點的應力狀態和應變狀態之間存在著一定的聯繫,這種聯繫與如何達到這種應力狀態和應變狀態的過程無關,即應力和應變之間存在一一對應的關係。若應力和應變呈線性關係,這個關係便叫作廣義胡克定律,各向同性材料的廣義胡克定律有兩種常用的數學形式:
![彈性力學[固體力學的重要分支]](/img/c/e0d/wZwpmL1ETNzMDOxETN2QTN1UTM1QDN5MjM5ADMwAjMwUzLxUzL3IzLt92YucmbvRWdo5Cd0FmLwE2LvoDc0RHa.jpg) 彈性力學[固體力學的重要分支]
彈性力學[固體力學的重要分支]和
![彈性力學[固體力學的重要分支]](/img/c/2b5/wZwpmLxEDO0ADM4kDN2QTN1UTM1QDN5MjM5ADMwAjMwUzL5QzLzUzLt92YucmbvRWdo5Cd0FmL0E2LvoDc0RHa.jpg) 彈性力學[固體力學的重要分支]
彈性力學[固體力學的重要分支]式中為應力分量;λ和 G為拉梅常數, G又稱剪下模量; E為楊氏模量(或彈性模量); v為泊松比(見材料的力學性能)。λ、 G、 E和 v四個常數之間存在下列聯繫:
![彈性力學[固體力學的重要分支]](/img/4/f68/wZwpmL3UDNxMTN1kDN2QTN1UTM1QDN5MjM5ADMwAjMwUzL5QzL2EzLt92YucmbvRWdo5Cd0FmLxE2LvoDc0RHa.jpg) 彈性力學[固體力學的重要分支]
彈性力學[固體力學的重要分支]式(3a)適用於已知應變求應力的問題,式(3b)的適用於已知應力求應變的問題。
③運動(或平衡)規律 處於運動(或平衡)狀態的物體,其中任一部分都遵守力學中的運動(或平衡)規律,即牛頓運動三定律,反映這個規律的數學方程有兩類:運動(或平衡)微分方程和載荷邊界條件。在笛卡兒坐標系中,運動(或平衡)微分方程為:
![彈性力學[固體力學的重要分支]](/img/6/55b/wZwpmL1QjN1YzM1ATN2QTN1UTM1QDN5MjM5ADMwAjMwUzLwUzLyEzLt92YucmbvRWdo5Cd0FmLyE2LvoDc0RHa.jpg) 彈性力學[固體力學的重要分支]
彈性力學[固體力學的重要分支]式中 t為時間; ρ為材料密度; f為作用在物體上的體力(外載荷的體積密度)分量。方程(5)實質上是從物體中隔離出來的一個微小平行六面體的運動方程。在平衡問題中,慣性力很小,忽略這些慣性力,便得到彈性力學中的平衡微分方程。
對於均勻而且各向同性的物體,應力分量可按式(3a)用應變分量表示,而應變分量又可按式(1)用位移分量表示。兩個公式依次代入方程(5),便得到用位移表示的運動微分方程:
![彈性力學[固體力學的重要分支]](/img/3/08c/wZwpmLzQTNzQDN1ATN2QTN1UTM1QDN5MjM5ADMwAjMwUzLwUzLxgzLt92YucmbvRWdo5Cd0FmLyE2LvoDc0RHa.jpg) 彈性力學[固體力學的重要分支]
彈性力學[固體力學的重要分支]式中 θ為體應變,即
![彈性力學[固體力學的重要分支]](/img/c/2ec/wZwpmL4ITO4kDO0ATN2QTN1UTM1QDN5MjM5ADMwAjMwUzLwUzLwgzLt92YucmbvRWdo5Cd0FmLxE2LvoDc0RHa.jpg) 彈性力學[固體力學的重要分支]
彈性力學[固體力學的重要分支]△為拉普拉斯算符,即
![彈性力學[固體力學的重要分支]](/img/d/5f2/wZwpmLyMDOwQDN1kDN2QTN1UTM1QDN5MjM5ADMwAjMwUzL5QzLwAzLt92YucmbvRWdo5Cd0FmL0E2LvoDc0RHa.jpg) 彈性力學[固體力學的重要分支]
彈性力學[固體力學的重要分支]類似地,在方程(6)中略去慣性力,便可得到用位移分量表示的平衡微分方程。
如果考慮物體一部分邊界 B是自由的,在它的上面有給定的外載荷,則根據作用力和反作用力大小相等方向相反的原理,在 B上有如下載荷邊界條件:
![彈性力學[固體力學的重要分支]](/img/5/941/wZwpmLwUjN4QDN3kDN2QTN1UTM1QDN5MjM5ADMwAjMwUzL5QzL4AzLt92YucmbvRWdo5Cd0FmLzE2LvoDc0RHa.jpg) 彈性力學[固體力學的重要分支]
彈性力學[固體力學的重要分支]![彈性力學[固體力學的重要分支]](/img/0/92c/wZwpmL3AzM1UzMyEDMyADN0UTMyITNykTO0EDMwAjMwUzLxAzL3UzLt92YucmbvRWdo5Cd0FmLyE2LvoDc0RHa.jpg) 彈性力學[固體力學的重要分支]
彈性力學[固體力學的重要分支]式中 i為邊界外法線方向的方向餘弦;等式右邊為給定的邊界載荷分量。
彈性力學問題的提法和求解
為了闡明一個彈件力學問題,需要說明物體的形狀和物體的各部分由什麼材料組成(直接給出物體各部分的廣義胡克定律當然更好);說明物體所承受的載荷,包括體積力 f、自由邊界上的載荷;說明此物體和其他物體的連線情況。例如,所考慮的對象是物體 Q,它在邊界 B和 B同另兩個物體 Q和 Q相連線。如果 Q的剛度比 Q大得多,則 B上各點的位移就基本上由 Q的位移決定。這樣,對 Q來說, B上各點的位移是由外界給定的,因而有位移邊界條件(2)。如果 Q的剛度比 Q小得多,則 Q基本上不能限制 B上各點的位移。這樣,對 Q來說, B可看作是自由的,因而有載荷的邊界條件(9)。如果 Q或 Q的剛度同 Q相差不多,要建立恰當的邊界條件就不那么容易,須就具體情況作細緻的分析。
對彈性力學的平衡問題,說明上述三個方面便可以了。但對彈性力學的動力問題,還需說明物體的初始狀態,即
當 t= t時,
![彈性力學[固體力學的重要分支]](/img/9/c43/wZwpmL0UDN0MTM3kDN2QTN1UTM1QDN5MjM5ADMwAjMwUzL5QzLyAzLt92YucmbvRWdo5Cd0FmLzE2LvoDc0RHa.jpg) 彈性力學[固體力學的重要分支]
彈性力學[固體力學的重要分支]式中 t為初始時間, u和 v分別為物體在初始時刻的位移和速度,它們應是給定的函式。
求解一個彈性力學問題,就是設法確定彈性體中各點的位移、應變和應力共15個函式。從理論上說,只有15個函式全部確定後,問題才算徹底解決。但在各種具體問題中,常常只關心其中的某幾個函式,有時甚至只關心物體的某些部位的某幾個函式。所以在實用上,常常不需要確定全部函式。求解時,可用實驗方法、數學方法,也可用實驗和數學相結合的方法。
實驗方法是用機械的、電的、光的以及其他手段在實物上或在模型上測量所需的量。許多複雜而難於計算的問題都是用實驗方法求解的(見實驗應力分析)。
數學方法就是根據幾何方程(1)、應力-應變關係(3a)或(3b)、運動(或平衡)微分方程(5)、邊界條件(2)和(9)以及動力問題中的初始條件(10),解出 u、、等15個函式。學方法的優點是提供的數據比較全面,但當前只適用於不太複雜的問題。這方面的研究構成了以數學方法為主要研究手段的數學彈性力學。
對於一些實用上重要的彈性力學問題,常需要同時用實驗和數學兩種方法求解,以保證結論的可靠性。
常用的數學方法
彈性力學中常用的數學方法可分分成兩類:
①精確解法 包括分離變數法和彈性力學的複變函數方法。彈性力學中的許多精確解是用分離變數法求得的。其步驟大致如下:根據物體的形狀,選擇一種合適的曲線坐標系,並寫出相應於該坐標系的彈性力學微分方程和邊界條件,如果微分方程中的變數能夠分離,通常便可求得問題的解。能用分離變數法求得精確解的問題有:無限和半無限體的問題,球體和球殼的問題,橢球腔的問題,圓柱和圓盤的問題等。
對於能化為平面調和函式或平面雙調和函式的問題,複變函數方法是一個有效的求解工具《柱體的扭轉和彎曲問題、平面應變和平面應力問題以及薄板彎曲問題中的許多重要精確解都是用複變函數法求得的。
②近似解法 為求解一些複雜的問題,在彈性力學中還發展了許多近似解法,能量法就是其中用得最多的一類方法,它把彈性力學問題化為數學中的變分問題(泛函的極值和駐值問題),然後再用瑞利-里茲法求近似解。能量法的內容很豐富,適應性很強。工程界當前廣泛使用的有限元法是能量法的一種新發展。差分法也是一種常用的近似解法,其要點是用差商近似地代替微商,從而把原有的微分方程近似地化為代數方程。此外,邊界積分方程、邊界元法和加權殘數法對解決某些問題也是有效的手段。
數學彈性力學的典型問題 有以下幾類:
①一般性理論 它探討解的共性和一般性的求解方法。一般性理論中,最核心的部分是能量原理(定理),包括虛功原理(虛位移原理、虛應力原理)、功的互等定理、最小勢能原理、最小余能原理、赫林格-瑞斯納二類變數廣義變分原理和胡海昌-鷲津久一郎三類變數廣義變分原理等。解的存在性、唯一性、解析性、平均值定理以及近似解的收斂性等,也都和能量原理有密切聯繫。這些一般性理論,是建立各種近似解法和建立工程結構實用理論的依據。
一般性理論的另一重要方面是未知函式的歸併理論,其主要內容是將彈性力學問題歸為求解少數幾個函式,這些函式常稱為應力函式和位移函式。
②柱體扭轉和彎曲 一個側面不受外力的細長柱體,在兩端面上的外力作用下會產生扭轉和彎曲。根據聖維南原理,柱體中間部分的應力狀態只與作用在端面上載荷的合力和合力矩有關,而與載荷的具體分布無關。因此,柱體中間部分的應力有以下的表達式:
![彈性力學[固體力學的重要分支]](/img/7/9e4/wZwpmL4QTN1kzN1ETN2QTN1UTM1QDN5MjM5ADMwAjMwUzLxUzLzgzLt92YucmbvRWdo5Cd0FmLyE2LvoDc0RHa.jpg) 彈性力學[固體力學的重要分支]
彈性力學[固體力學的重要分支]這裡的 x、 y軸為橫截面的兩個主軸; z軸平行於柱體的母線;為應力分量, A為橫截面的面積; I和 I為橫截面對 x軸和 y軸的慣性矩(見截面的幾何性質); N、 M和 M分別為作用在截面上的軸向合力、對 x軸和 y軸的彎矩。彎矩 M、 M是坐標 z的線性函式,可用材料力學的方法求得。式(11)給出的與材料力學的解相同,但給出的剪應力比材料力學的結果精確。決定的問題最後可歸為求解一個平面調和函式的邊值問題。
③平面問題 平面問題是彈性力學中發展得比較成熟,套用得比較廣的一類問題。平面問題可分為平面應力問題和平面應變問題。兩者的套用對象不同,但都可歸為相同的數學問題——平面雙調和函式的邊值問題.
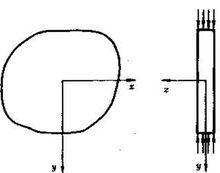 圖1 平面應力問題
圖1 平面應力問題平面應力問題適用於薄板。若在薄板的兩個表面上無外力,而在側面上有沿厚度均勻分布的載荷(圖1),則薄板中的位移和應力有如下特點:
![彈性力學[固體力學的重要分支]](/img/b/c36/wZwpmL1YzN0gTO0ATN2QTN1UTM1QDN5MjM5ADMwAjMwUzLwUzLzIzLt92YucmbvRWdo5Cd0FmLzE2LvoDc0RHa.jpg) 彈性力學[固體力學的重要分支]
彈性力學[固體力學的重要分支]且以及 x 、y方向的位移 u、v都與坐標 z無關。對於各向同性材料,上述五個不等於零的量可以用一個應力函式 φ( x,y)(艾里應力函式)表示為:
![彈性力學[固體力學的重要分支]](/img/2/bb8/wZwpmL1YjN2czN5ETN2QTN1UTM1QDN5MjM5ADMwAjMwUzLxUzLyIzLt92YucmbvRWdo5Cd0FmLzE2LvoDc0RHa.jpg) 彈性力學[固體力學的重要分支]
彈性力學[固體力學的重要分支]而應力函式 φ是一個平面雙調和函式,即
![彈性力學[固體力學的重要分支]](/img/7/e73/wZwpmL0ETMxYDOyETN2QTN1UTM1QDN5MjM5ADMwAjMwUzLxUzLwYzLt92YucmbvRWdo5Cd0FmLzE2LvoDc0RHa.jpg) 彈性力學[固體力學的重要分支]
彈性力學[固體力學的重要分支]平面應變問題適用於長柱體的中間部分。若柱體的兩端面固定不動,而作用在側面上的載荷和坐標 z無關,且合力及合力矩等於零(圖2),則柱體中間部分的應力和位移有如下特點:
![彈性力學[固體力學的重要分支]](/img/1/c84/wZwpmLyATN0cDMyETN2QTN1UTM1QDN5MjM5ADMwAjMwUzLxUzL3gzLt92YucmbvRWdo5Cd0FmLwE2LvoDc0RHa.jpg) 彈性力學[固體力學的重要分支]
彈性力學[固體力學的重要分支]縱向位移 ω=0,且、 u、 v與坐標 z無關。對於各向同性的材料,上述五個不等於零的量也可用一個雙調和函式 φ表示為公式(13),不過須將其中的 E和 v分別代以
![彈性力學[固體力學的重要分支]](/img/8/14e/wZwpmL2QzNzkjM1ATN2QTN1UTM1QDN5MjM5ADMwAjMwUzLwUzL0gzLt92YucmbvRWdo5Cd0FmL0E2LvoDc0RHa.jpg) 彈性力學[固體力學的重要分支]
彈性力學[固體力學的重要分支]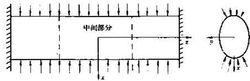 圖2 平面應變問題
圖2 平面應變問題④變截面軸扭轉變截面軸受扭時,在截面的過渡區(圖3)常有應力集中現象。分析這類問題以取圓柱坐標系(r,θ,z)為方便。在圓柱坐標系中的位移分量和應力分量分別記為u、v、w和
![彈性力學[固體力學的重要分支]](/img/9/5fe/wZwpmLyITN5EzNxETN2QTN1UTM1QDN5MjM5ADMwAjMwUzLxUzLxIzLt92YucmbvRWdo5Cd0FmLyE2LvoDc0RHa.jpg) 彈性力學[固體力學的重要分支]
彈性力學[固體力學的重要分支]這類問題的力學特點是: u=w=0和
![彈性力學[固體力學的重要分支]](/img/a/596/wZwpmLygTNxcjN0kDN2QTN1UTM1QDN5MjM5ADMwAjMwUzL5QzLzQzLt92YucmbvRWdo5Cd0FmLyE2LvoDc0RHa.jpg) 彈性力學[固體力學的重要分支]
彈性力學[固體力學的重要分支]![彈性力學[固體力學的重要分支]](/img/f/9c8/wZwpmL4gjMwYjNykDN2QTN1UTM1QDN5MjM5ADMwAjMwUzL5QzLxgzLt92YucmbvRWdo5Cd0FmL0E2LvoDc0RHa.jpg) 彈性力學[固體力學的重要分支]
彈性力學[固體力學的重要分支]![彈性力學[固體力學的重要分支]](/img/9/50f/wZwpmL0UTN3ITN1ATN2QTN1UTM1QDN5MjM5ADMwAjMwUzLwUzLwUzLt92YucmbvRWdo5Cd0FmLzE2LvoDc0RHa.jpg) 彈性力學[固體力學的重要分支]
彈性力學[固體力學的重要分支]![彈性力學[固體力學的重要分支]](/img/f/9c8/wZwpmL4gjMwYjNykDN2QTN1UTM1QDN5MjM5ADMwAjMwUzL5QzLxgzLt92YucmbvRWdo5Cd0FmL0E2LvoDc0RHa.jpg) 彈性力學[固體力學的重要分支]
彈性力學[固體力學的重要分支]![彈性力學[固體力學的重要分支]](/img/9/50f/wZwpmL0UTN3ITN1ATN2QTN1UTM1QDN5MjM5ADMwAjMwUzLwUzLwUzLt92YucmbvRWdo5Cd0FmLzE2LvoDc0RHa.jpg) 彈性力學[固體力學的重要分支]
彈性力學[固體力學的重要分支]v、和與坐標z無關。上述不等於零的兩個剪應力和可用一個應力函式(r,z)表示為:
![彈性力學[固體力學的重要分支]](/img/f/6a4/wZwpmLzYDMyEjM3kDN2QTN1UTM1QDN5MjM5ADMwAjMwUzL5QzLwEzLt92YucmbvRWdo5Cd0FmL0E2LvoDc0RHa.jpg) 彈性力學[固體力學的重要分支]
彈性力學[固體力學的重要分支]而滿足下列偏微分方程:
![彈性力學[固體力學的重要分支]](/img/6/c1f/wZwpmL1EDM4IjN0ATN2QTN1UTM1QDN5MjM5ADMwAjMwUzLwUzLwUzLt92YucmbvRWdo5Cd0FmLxE2LvoDc0RHa.jpg) 彈性力學[固體力學的重要分支]
彈性力學[固體力學的重要分支]這類問題最後歸為方程(15)的邊值問題。
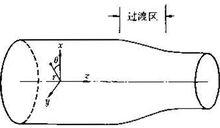 圖3 變截面軸的過渡區示意圖
圖3 變截面軸的過渡區示意圖![彈性力學[固體力學的重要分支]](/img/f/9c8/wZwpmL4gjMwYjNykDN2QTN1UTM1QDN5MjM5ADMwAjMwUzL5QzLxgzLt92YucmbvRWdo5Cd0FmL0E2LvoDc0RHa.jpg) 彈性力學[固體力學的重要分支]
彈性力學[固體力學的重要分支]![彈性力學[固體力學的重要分支]](/img/9/50f/wZwpmL0UTN3ITN1ATN2QTN1UTM1QDN5MjM5ADMwAjMwUzLwUzLwUzLt92YucmbvRWdo5Cd0FmLzE2LvoDc0RHa.jpg) 彈性力學[固體力學的重要分支]
彈性力學[固體力學的重要分支]![彈性力學[固體力學的重要分支]](/img/f/f36/wZwpmLwYTN0QTN2kDN2QTN1UTM1QDN5MjM5ADMwAjMwUzL5QzL2AzLt92YucmbvRWdo5Cd0FmLyE2LvoDc0RHa.jpg) 彈性力學[固體力學的重要分支]
彈性力學[固體力學的重要分支]![彈性力學[固體力學的重要分支]](/img/9/94f/wZwpmL3ETMwkjN5kDN2QTN1UTM1QDN5MjM5ADMwAjMwUzL5QzL2EzLt92YucmbvRWdo5Cd0FmLxE2LvoDc0RHa.jpg) 彈性力學[固體力學的重要分支]
彈性力學[固體力學的重要分支]![彈性力學[固體力學的重要分支]](/img/c/f51/wZwpmLzIDOzITMxATN2QTN1UTM1QDN5MjM5ADMwAjMwUzLwUzL0QzLt92YucmbvRWdo5Cd0FmLxE2LvoDc0RHa.jpg) 彈性力學[固體力學的重要分支]
彈性力學[固體力學的重要分支]![彈性力學[固體力學的重要分支]](/img/0/dd1/wZwpmLwgzN2UzN5ATN2QTN1UTM1QDN5MjM5ADMwAjMwUzLwUzL0AzLt92YucmbvRWdo5Cd0FmL0E2LvoDc0RHa.jpg) 彈性力學[固體力學的重要分支]
彈性力學[固體力學的重要分支]⑤迴轉體的軸對稱變形各向同性的迴轉體在軸對稱載荷作用下,必然產生軸對稱的變形。在圓柱坐標系(r,θ,z)中,軸對稱變形的特點是:v=0,=,且u、w、、、和與坐標θ無關。上述不等於零的六個量,可以用一個位移函式(x,y)表示為:
![彈性力學[固體力學的重要分支]](/img/a/4ef/wZwpmLygTN2YTN2ATN2QTN1UTM1QDN5MjM5ADMwAjMwUzLwUzL3YzLt92YucmbvRWdo5Cd0FmLwE2LvoDc0RHa.jpg) 彈性力學[固體力學的重要分支]
彈性力學[固體力學的重要分支]其中△是軸對稱的拉昔拉斯算符,即
![彈性力學[固體力學的重要分支]](/img/a/41e/wZwpmL2ITO0gjN1ATN2QTN1UTM1QDN5MjM5ADMwAjMwUzLwUzL0UzLt92YucmbvRWdo5Cd0FmLyE2LvoDc0RHa.jpg) 彈性力學[固體力學的重要分支]
彈性力學[固體力學的重要分支]而是軸對稱的雙調和函式,即
![彈性力學[固體力學的重要分支]](/img/8/3f4/wZwpmLxATM0kDN0ATN2QTN1UTM1QDN5MjM5ADMwAjMwUzLwUzLyUzLt92YucmbvRWdo5Cd0FmLxE2LvoDc0RHa.jpg) 彈性力學[固體力學的重要分支]
彈性力學[固體力學的重要分支]⑥工程結構元件的實用理論 從廣義上說,各種工程結構元件的實用理論(如桿、板、殼的實用理論)都是彈性力學的特殊分支,而且是最有實用價值的分支。這些實用理論分別依據結構元件形狀及其受力的特點,對位移分布作一些合理的簡化假設,對廣義胡克定律也作相應的簡化。這樣,就能使數學方程既得到充分簡化又保留了主要的力學特性。從彈性力學看,這些結構元件的實用理論都是近似理論,其近似性大多表現為按照這些理論計算得到的應力和應變不能嚴格滿足胡克定律。
![彈性力學[固體力學的重要分支] 彈性力學[固體力學的重要分支]](/img/c/05e/nBnauM3XyYTN5MzM2ETN2QTN1UTM1QDN5MjM5ADMwAjMwUzLxUzLwgzLt92YucmbvRWdo5Cd0FmLyE2LvoDc0RHa.jpg)
