原理
 弦截法
弦截法 弦截法
弦截法 弦截法
弦截法 弦截法
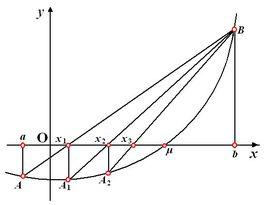
弦截法方程 實數解 的幾何意義是曲線 與 軸交點的橫坐標。
 弦截法
弦截法 弦截法
弦截法 弦截法
弦截法 弦截法
弦截法 弦截法
弦截法弦截法的原理是 以直代曲即用弦(直線)代替曲線求方程的近似解,也就是利用對應的弦 與 軸的交點橫坐標來作為曲線弧 與 軸的交點橫坐標 的近似值。
疊代
確定含根區間
 弦截法
弦截法 弦截法
弦截法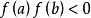 弦截法
弦截法 弦截法
弦截法 弦截法
弦截法若 在區間 上連續, ,則稱區間 為方程 的含根區間。
弦截法的近似根公式
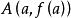 弦截法
弦截法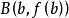 弦截法
弦截法 弦截法
弦截法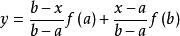 弦截法
弦截法 弦截法
弦截法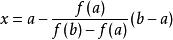 弦截法
弦截法 弦截法
弦截法 弦截法
弦截法 弦截法
弦截法由於過 和 兩點的直線 的方程為 ,將直線與 軸交點的橫坐標 取作方程 在含根區間 上解 的近似值。
疊代必要性
 弦截法
弦截法 弦截法
弦截法使用弦截法是可以得到方程 在含根區間 上的近似解。但是只用一次弦截法得到近似解誤差可能相當大,精度可能不能滿足要求。所以要根據第一次弦截法的結果進行再次、多次疊代。
 弦截法
弦截法 弦截法
弦截法 弦截法
弦截法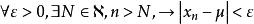 弦截法
弦截法當函式 滿足了一定的條件後,經過逐次疊代得到的近似解數列 是收斂,且收斂於方程的解 ,根據極限的思想, ,經過有限次疊代就能滿足精度要求的近似解。
疊代規則
進行多次疊代的本質是反覆“ 縮小的含根區間,新的 縮小的含根區間上求新的近似根 ”。
疊代的操作規則是
 弦截法
弦截法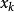 弦截法
弦截法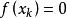 弦截法
弦截法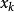 弦截法
弦截法(1)記第 次弦截法下的近似根為 ,如果 ,那么 就是方程的根,疊代結束。
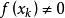 弦截法
弦截法 弦截法
弦截法(2)如果,根據 的正負號按新求出照如下規則操作:
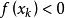 弦截法
弦截法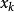 弦截法
弦截法 弦截法
弦截法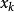 弦截法
弦截法 弦截法
弦截法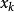 弦截法
弦截法 弦截法
弦截法 弦截法
弦截法如果 ,則將 記為 (將 賦值給 ),反之將 記為 ,可以得到新的縮小了的含根區間 。
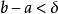 弦截法
弦截法 弦截法
弦截法(3)判斷精度要求是否得到滿足,如果 ( 為給定的精度要求),疊代結束。
 弦截法
弦截法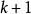 弦截法
弦截法(4)如果精度要求沒得到滿足,那么在新的含根區間上繼續用弦截法求出次近似解
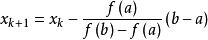 弦截法
弦截法如此循環反覆,直到滿足要求。
特殊條件下的疊代公式
 弦截法
弦截法 弦截法
弦截法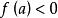 弦截法
弦截法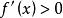 弦截法
弦截法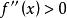 弦截法
弦截法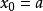 弦截法
弦截法若函式在區間上連續,,且,取作為初始近似解,那么弦截法的疊代公式為
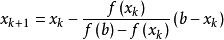 弦截法
弦截法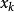 弦截法
弦截法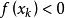 弦截法
弦截法這是因為對於每次疊代得到的總是有,新的含根區間右端點始終不變,左端點不斷更新。
充分條件
 弦截法
弦截法 弦截法
弦截法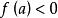 弦截法
弦截法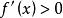 弦截法
弦截法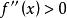 弦截法
弦截法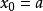 弦截法
弦截法若函式 在區間 上連續, , 且 ,取 ,那么
(1)弦截法的疊代公式為
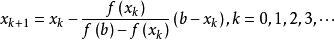 弦截法
弦截法 弦截法
弦截法(2)數列 收斂;
 弦截法
弦截法 弦截法
弦截法 弦截法
弦截法 弦截法
弦截法(3)數列 收斂於方程 在區間 上的唯一實數根 。
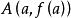 弦截法
弦截法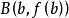 弦截法
弦截法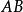 弦截法
弦截法 弦截法
弦截法 弦截法
弦截法證明 第一次弦截法是取以 和 為端點的弦 與 軸交點的橫坐標為方程 的第一次近似解
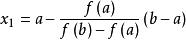 弦截法
弦截法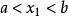 弦截法
弦截法這裡有 。由凸函式性質可知
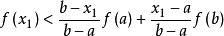 弦截法
弦截法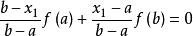 弦截法
弦截法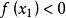 弦截法
弦截法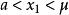 弦截法
弦截法而 ,所以 ,由函式單調性可得 。
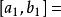 弦截法
弦截法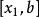 弦截法
弦截法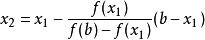 弦截法
弦截法於是得到方程新的含根區間為 ,及新的近似解 。
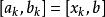 弦截法
弦截法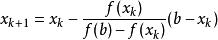 弦截法
弦截法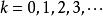 弦截法
弦截法利用數學歸納法(從略)可得: , ,
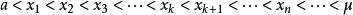 弦截法
弦截法以及 。
 弦截法
弦截法 弦截法
弦截法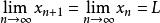 弦截法
弦截法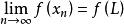 弦截法
弦截法於是可知數列 是單調增加有上界,所以收斂。設其極限為 ,即 ,根據函式的連續性又可知 。
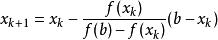 弦截法
弦截法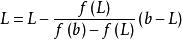 弦截法
弦截法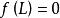 弦截法
弦截法 弦截法
弦截法 弦截法
弦截法 弦截法
弦截法 弦截法
弦截法在等式 兩邊同求極限得, ,即可得 。證得數列 收斂於方程 在區間 上的唯一實數根 。
C語言代碼
//弦截法求x*x*x-5*x*x+16*x-80=0的根
求x^3-5x^2+16x-80的值:
#include<math.h>
#include<stdio.h>
float f(float x)
{ //計算f(x)的值
return x*(x*x-5*x+16)-80;
}
float point(float x1,float x2)
{
//計算與x軸交點的x值
return (x1*f(x2)-x2*f(x1))/(f(x2)-f(x1));
}
void main()
{
//輸入兩個數x1,x2
float x1,x2,x;
do
{
printf("輸入兩個數x1,x2:");
scanf("%f%f",&x1,&x2);
}
while (f(x1)*f(x2) >= 0); // 當輸入兩個數大於0為真時,繼續重新輸入
//關鍵循環步驟:
do
{
x=point(x1,x2);//得到交點的值
if(f(x)*f(x1)>0)
x1=x;//新的x1
else
x2=x;
}
while (fabs(f(x)) > 0.0001); //0.0001為取值精度
printf("一個解為%f\n",x);
}
定義函式
function y=f(t)
y=f(t); %函式f(t)的表達式
主程式
i=0; %疊代此處記數
t1=t1; %疊代初值t1
t2=t2; %疊代初值t2
while i<=100;
y=t2-f(t2)/(f(t2)-f(t1))*(t2-t1); %弦截法疊代格式
if abs(y-t2)>10^(-6); %收斂判據
t1=t2;
t2=y
else break
end
i=i+1;
end
fprintf('\n%s%.6f\t%s%d%','泡點溫度t=",y,"疊代次數i=",i)%輸出結果