基本概念
弓形由弦及其所對的弧組成的圓形叫做弓形。
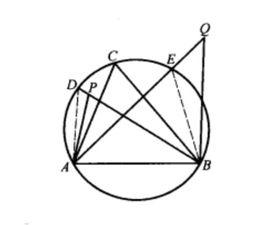
弓形角：（1）由於同弧或等弧所對的圓周角相等，所以把此弧所對的圓周角叫做此弧所含的圓周角，或叫此弧所含的弓形角。（2）弓形中的弧上任一點與它的弦的兩端點所成的角叫這弓形的弧所含的弓形角。 （3）弓形角是指頂點在弓形的弧上，兩邊分別通過該弓形的弦的兩端的角，也叫弓形弧的內接角。如圖1，∠APB就是弓形角。
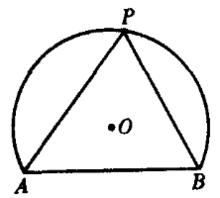圖1弓形角的作法
弓形角(在已知線段上作含有已知圓周角的弧)有一個實際問題：如圖2，A、B是海上的兩個燈塔，在對著AB的一條弧內有許多暗礁，這條弧所含的圓周角是α，怎樣在地圖上劃出這個危險區?這個問題就是在已知線段上作含有已知圓周角（弓形角）的弧的問題 。
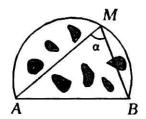圖2已知 線段AB和∠α(如圖3)。
求作 在AB上含有等於∠α的圓周角的弧。
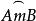弓形角 弓形角 弓形角作法 作∠BAC=∠α；作AB垂直平分線DE；作AF ⊥AC，交DE於O；以O為圓心，OA為半徑作弧，使和AC在AB的兩旁，則就是所求作的弧 。
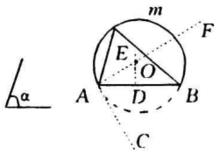圖3相關定理
定理1 同一個弓形的所有的弓形角都相等。
已知：∠ACB、∠ADB是弓形AB內任意兩個弓形角。
求證：∠ACB=∠ADB。
證明：因為∠ACB、∠ADB都等於∠AOB的一半，所以他們相等，而且其他弓形角也是如此，所以同一個弓形的所有的弓形角都相等 。
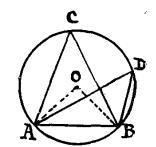圖4推論 弓形內一點，對於弓形的弦所張的角比弓形角大，弓形外一點和弓形在它的弦的同側，那么這一點對弦所張的角小於弓形角。（從弓形弧內一點至其弦之兩端所聯線段之夾角，大於此弓形之弓形角；從弓形弧外一點至其弦之兩端所聯線段之夾角，小於此弓形之弓形角。）
證明：因為∠APB>∠ACB，而∠ACB是弓形角，所以∠APB大於弓形角，
又∠AQB<∠ADB，
所以∠AQB小於弓形角 。
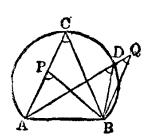圖5定理2 半圓內所有弓形角都是直角。
證明：假定∠ACB是半圓內的任何一個弓形角，那么它等於弧AEB上圓心角的一半，
但是∠AOB=180°（O為圓心），
所以∠ACB=90°，故∠ACB為直角 。
