簡介
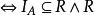 序關係
序關係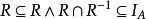 序關係
序關係偏序關係,亦稱序關係、弱偏序關係、半序關係,是一種重要的二元關係。指集合A有自反性、反對稱性和傳遞性的二元關係R,A稱為偏序集。偏序關係常用記號≤表示(仍讀作小於或等於)。a≤b意即aRb。偏序關係可用符號表示為:R是A的偏序關係。。
定義1,設P是集合,P上的二元關係“≤”滿足以下三個條件,則稱“≤”是P上的偏序關係(或部分序關係):
(1)自反性:a≤a,∀a∈P;
(2)反對稱性:∀a,b∈P,若a≤b且b≤a,則a=b;
(3)傳遞性:∀a,b,c∈P,若a≤b且b≤c,則a≤c;
特點
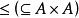 序關係
序關係偏序關係有下列特點:
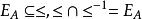 序關係
序關係1、對角集;
2、≤ 的矩陣(r)的主對角線上的元素全是1;當 i ≠ j 時,r·r = 0,當 r = r = 1時,r=1;
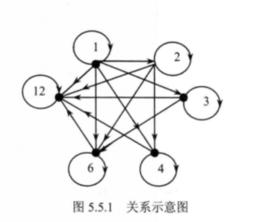
3、≤ 的箭頭圖上每一點有一箭頭從自己出發而指向自己。如有箭頭從a指向b,從b指向c,就有箭頭從a指向c,任何兩點間無雙箭頭。
偏序關係的逆關係≥一定是偏序關係,偏序關係一定是擬序關係。1880年,皮爾斯(Perice,C.S.)首先系統地討論了偏序關係,而關於偏序的術語是由豪斯多夫(Hausdorff,F.)從1914年引進的。
擬序關係
 序關係
序關係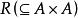 序關係
序關係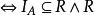 序關係
序關係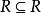 序關係
序關係也叫做偽序關係或前序關係,一種重要的二元關係。指集合A上的自反的與傳遞的二元關係R,A稱為擬續集,即關係是擬序關係。。
擬序關係有下列特點:
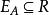 序關係
序關係1、對角集,且當<a,b>∈R,<b,c>∈R時,<a,c>∈R。
2、R的矩陣(r)的主對角線上的元素全是1,且當 r= r= 1時,r=1;
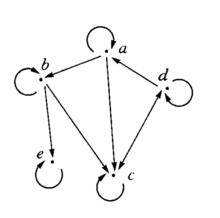
3、R的箭頭圖上,每個元素有一個從自己出發又指向自身的箭頭,且在有a到b的箭頭,b到c的箭頭時,就有a到c的箭頭,如右圖的關係箭頭表示的是集A={a,b,c,d,e}上的一個擬序。
擬序關係的逆關係一定是擬序的,反對稱的擬序關係是偏序關係,但擬序關係可以不是偏序關係。例如,圖中表示的擬序就不是偏序,因為cRd且dRc,但c≠d。