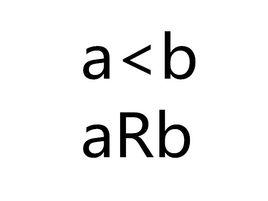基本介紹
嚴格偏序關係是一種重要的偏序關係,指集合A上的反自反的、傳遞的和非對稱的二元關係R,A稱為嚴格偏序集.嚴格偏序關係常記以特殊的記號<,a<b意即aRb 。
【例1】 自然數集N、整數Z、有理數集Q和實數集R上的小於關係,集合之間的真包含關係等等,都是嚴格偏序關係。
嚴格偏序關係和偏序關係之間有密切的聯繫,如果<是一個嚴格偏序關係,那么相應的偏序關係就可以定義為:x≤y若且唯若x<y或者x=y。反之,如果≤是一個偏序關係,與此相應的嚴格偏序關係就可以定義為:x<y若且唯若x≤y並且x≠y。
另外,集合X上的嚴格偏序關係<必是反對稱的。事實上,如果<不是反對稱的,則存在x∈X和y∈X使得x<y並且y<x,因為<是一個嚴格偏序,所以<必具有傳遞性,由x<y並且y<x可得x<x,這與<是反自反的相矛盾 。
嚴格偏序關係的特點
嚴格偏序關係<(⊆A×A)有下列特點:
1.E∩<=∅,(<°<)⊆<,且〈a,b〉∈<時,〈b,a〉∉<。
2.<的矩陣M=(r)的主對角線上全是零,對任何i,j,r·r=0,且r=r=1時,r=1。
3.<的箭頭圖上每一個點都沒有從自己出發指向自身的箭頭,不同兩點間沒有雙向箭頭,且若有從a向b、從b向c的箭頭就有從a向c的箭頭 。