序列空間定義
 序列空間
序列空間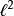 序列空間
序列空間更一般的希爾伯特空間都是無窮維的,假設 是一個任意集合,可以定義其上的 序列空間,記為
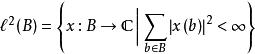 序列空間
序列空間此空間在定義如下內積後,成為一個希爾伯特空間:
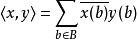 序列空間
序列空間 序列空間
序列空間 序列空間
序列空間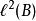 序列空間
序列空間 序列空間
序列空間 序列空間
序列空間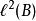 序列空間
序列空間 序列空間
序列空間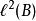 序列空間
序列空間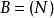 序列空間
序列空間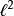 序列空間
序列空間其中 和 是 中的任意元素。在這個定義中, 並非一定要是可數的,在 不可數之情形下, 不是可分(separable)的。在下面更具體的例子中,所有的希爾伯特空間在選定適當的 的情況下,都可以表示成為 的一個同構空間。特別地,當 的時候,可以將其簡單記為 。
常見空間定義
歐幾里得空間
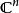 序列空間
序列空間及其上的內積
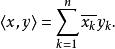 序列空間
序列空間構成了一個希爾伯特空間,其中短橫線表示一個複數的復共軛。
勒貝格空間
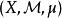 序列空間
序列空間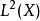 序列空間
序列空間 序列空間
序列空間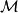 序列空間
序列空間 序列空間
序列空間 序列空間
序列空間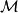 序列空間
序列空間 序列空間
序列空間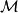 序列空間
序列空間勒貝格空間( 這裡指 空間 )是指定義在測度空間上的函式空間,其中 代表函式的定義域, 的元素是 上的子集族,為 一個 代數,一般把 稱作可測空間(measurable space),而 是 上的測度。
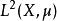 序列空間
序列空間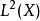 序列空間
序列空間 序列空間
序列空間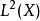 序列空間
序列空間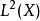 序列空間
序列空間更仔細的說, ( 簡寫做 ) 表示 上所有平方可積(square-integrable)的複數值的可測函式的集合。平方可積表示該函式的絕對值的平方的積分是有限的。要注意的是在 空間裡,對於幾乎處處( almost everywhere )相同的函式,也就是說如果兩函式只在一個測度為0的集合上不相等,我們把這兩函式當做在 中相同的元素。
此時兩個函式f和g的內積定義為
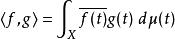 序列空間
序列空間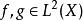 序列空間
序列空間因為,所以這內積的定義沒有問題。
但需要證明的是:
•此空間在此內積下是完備的。
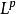 序列空間
序列空間這個證明可以在相關的書籍中找到,與此例相關的內容可以參看關於空間的著作 。
索伯列夫空間
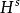 序列空間
序列空間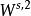 序列空間
序列空間索伯列夫空間一般表示為或者是希爾伯特空間的另一個重要實例,它多被套用於偏微分方程的研究 。
