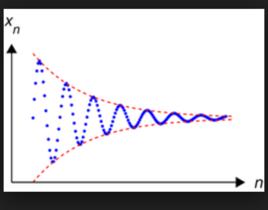
簡介
柯西列的定義依賴於距離的定義,所以只有在度量空間(metric space)中柯西列才有意義。在更一般的一致空間(uniform space)中,可以定義更為抽象的柯西濾子(Cauchy filter)和柯西網(Cauchy net)。
一個重要性質是,在完備空間(complete space)中,所有的柯西列都有極限,這就讓人們可以在不求出這個極限(如果存在)的情況下,利用柯西列的判別法則證明該極限是存在的。柯西列在構造具有完備性的代數結構的過程中也有重要價值,如構造實數。
複數序列
一個複數序列
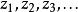 柯西序列
柯西序列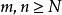 柯西序列
柯西序列被稱為 柯西列,如果對於任何正實數r>0,存在一個正整數N使得對於所有的整數,都有
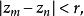 柯西序列
柯西序列其中的豎線表示絕對值或模。
類似地,我們可以定義實數的柯西列。
度量空間中
為了將柯西列的定義推廣到一般的度量空間,必須將絕對值替換為該度量空間中的距離。
形式上說,給定任何一個度量空間(M,d),一個序列
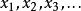 柯西序列
柯西序列被稱為 柯西列,如果對於任何正實數r>0,存在一個正整數N使得對於所有的整數m,n>N,都有
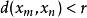 柯西序列
柯西序列其中d(x,y)表示x和 y之間的距離。
直觀上說,一個序列中的元素越來越靠近似乎說明這個序列必然在這個度量空間存在一個極限,而事實上在某些情況下這個結論是不對的。
例子
 柯西序列
柯西序列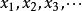 柯西序列
柯西序列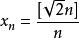 柯西序列
柯西序列 柯西序列
柯西序列 柯西序列
柯西序列 柯西序列
柯西序列對於有絕對值作為範數的有理數空間,定義數列:滿足:。這個數列趨於,但不屬於,因此這個數列不收斂。
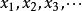 柯西序列
柯西序列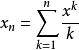 柯西序列
柯西序列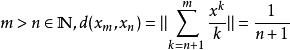 柯西序列
柯西序列對於所有多項式組成的空間,定義每個多項式的範數是其係數絕對值的最大值,兩個多項式之間的距離則是它們的差的範數。考慮多項式列:,滿足:。這個多項式列中,對任意,趨於零,因此它是一個柯西列。但這個柯西列顯然不收斂,因為它的元素次數趨於無窮。
性質
完備性
一個度量空間X中的所有柯西數列都會收斂到X 中的一點 ,那么X被稱為是一個完備空間。
•例子:實數
實數是完備的,而且標準的實數構造包含有理數的柯西列。
•反例:有理數
有理數Q在通常定義的距離意義下不是完備的:
存在某個由有理數組成的序列,收斂到某個無理數,所以這數列在有理數這空間是不收斂的。
例如:
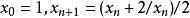 柯西序列
柯西序列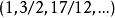 柯西序列
柯西序列 柯西序列
柯西序列如下定義的序列:,即。可以證明這個序列收斂到一個無理數。
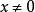 柯西序列
柯西序列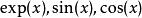 柯西序列
柯西序列對於每個給定的而言,以下函式的值都可以表示為一個有理數序列的極限,但當x為有理數時,這個值卻是無理數。
其他性質
任何收斂數列必然是柯西列,任何柯西列必然是有界序列。
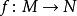 柯西序列
柯西序列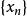 柯西序列
柯西序列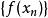 柯西序列
柯西序列如果是一個由度量空間 M到度量空間N的一致連續的映射,並且是 M中的柯西列,那么也必然是N中的柯西列。
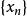 柯西序列
柯西序列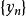 柯西序列
柯西序列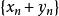 柯西序列
柯西序列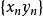 柯西序列
柯西序列如果和是有理數、實數或複數構成的柯西列,那么和也是柯西列。
推廣
拓撲向量空間
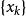 柯西序列
柯西序列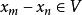 柯西序列
柯西序列在一個拓撲向量空間X中同樣可以定義一個柯西列:在X選擇一個0局部基B,如果對於B中的任何元素V,存在一個正整數N使得對於任意的m,n>N而言,序列滿足,那么這個序列就稱為一個柯西列。
如果這個拓撲向量空間X上有恰好可以引入一個平移不變度量d,那么上述方法定義的柯西列和利用這個度量d定義的柯西列是等價的。
群中
在一個群中,同樣可以定義柯西列:
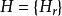 柯西序列
柯西序列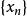 柯西序列
柯西序列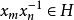 柯西序列
柯西序列令表示一列有限指標的遞減的G的正規子群,那么群G中一個序列稱為柯西列(對於上述 H而言),若且唯若對於任意的r,存在正整數N使得對於任意的 m,n>N,都有。
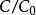 柯西序列
柯西序列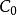 柯西序列
柯西序列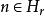 柯西序列
柯西序列如果用C表示所有的這樣定義的柯西列組成的集合,那么C在序列點點相乘的意義下構成一個新的群。而且,即所有空序列(對於任意r,存在N使得對於任意n>N,都有)構成了C的正規子群。而商群稱為G相對於H的完備化。
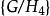 柯西序列
柯西序列可以證明,這個完備化同構與序列的逆向極限同構。
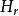 柯西序列
柯西序列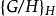 柯西序列
柯西序列如果H是個共尾序列(即任何有限的正規子群均包含某個),那么這個完備化在與的逆極限同構的意義下是規範的,這裡的H跑遍所有有限的正規子群。