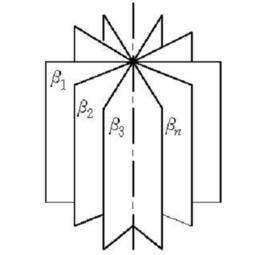
有軸平面束
定義
空間中通過同一直線的所有平面的集合叫做有軸平面束,那條直線叫做平面束的軸。
方程推導
通過空間直線L的平面有無窮多個,將通過空間直線L的所有平面的集合稱為過直線L的的平面束,設直線L的一般式方程為
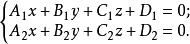 平面束
平面束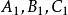 平面束
平面束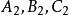 平面束
平面束其中係數 與 不成比例,構造一個三元一次方程:
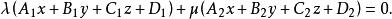 平面束
平面束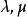 平面束
平面束其中 為任意實數,則上式可寫成
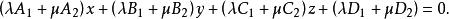 平面束
平面束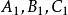 平面束
平面束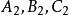 平面束
平面束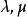 平面束
平面束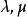 平面束
平面束由於係數與 與 不成比例,所以對於任何實數 ,上述方程的一次項係數不全為零,從而它表示一個平面,對於不同的 值,所對應的平面也不同,而且這些平面都通過直線L,也就是說,這個方程表示通過直線L的一族平面,另一方面,任何通過直線L的平面也一定包含在上述通過L的平面族中,因此,上述方程
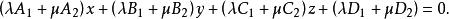 平面束
平面束就是通過直線L的平面束方程。
特殊情況
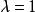 平面束
平面束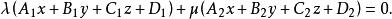 平面束
平面束特別地,取 時,上述方程 化為
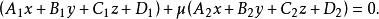 平面束
平面束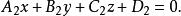 平面束
平面束上式表示除了平面 之外的過直線L的平面束。
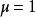 平面束
平面束取 時化為
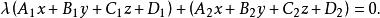 平面束
平面束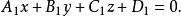 平面束
平面束表示除了平面 之外的過直線L的平面束。
平行平面束
定義
空間中平行於同一平面的所有平面的集合叫做平行平面束。
方程推導
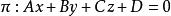 平面束
平面束由平面 決定的平行平面束的方程為
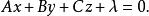 平面束
平面束 平面束
平面束其中 為任意實數。
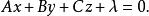 平面束
平面束 平面束
平面束 平面束
平面束 平面束
平面束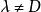 平面束
平面束 平面束
平面束證明 首先,對任意的實數A,方程 總表示由平面 決定的平行平面束中的平面,當 =D時,它表示平面 ;當 時,它表示與平面 平行的平面。
 平面束
平面束 平面束
平面束 平面束
平面束反過來,對於由平面 決定的平行平面束中任一平面 ',它的方程總可表示成 方程
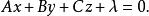 平面束
平面束 平面束
平面束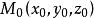 平面束
平面束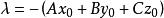 平面束
平面束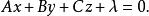 平面束
平面束的形式,事實上,若取平面 ’上一點 ,則可取 ,使平面'的方程表示成方程 的形式:
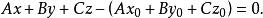 平面束
平面束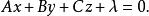 平面束
平面束 平面束
平面束綜上,方程 是由平面 決定的平行平面束的方程。