定義
 平均變化率
平均變化率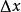 平均變化率
平均變化率 平均變化率
平均變化率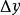 平均變化率
平均變化率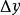 平均變化率
平均變化率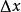 平均變化率
平均變化率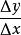 平均變化率
平均變化率 平均變化率
平均變化率 平均變化率
平均變化率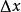 平均變化率
平均變化率一個函式在處有增量,則也會有相應的增量,那么我們就稱與的增量的比為函式在處增量為的平均變化率。
公式
 平均變化率
平均變化率 平均變化率
平均變化率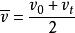 平均變化率
平均變化率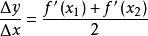 平均變化率
平均變化率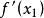 平均變化率
平均變化率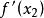 平均變化率
平均變化率 平均變化率
平均變化率 平均變化率
平均變化率 平均變化率
平均變化率 平均變化率
平均變化率註:高中數學課本提到,位移對時間的導數是速度,那么根據物理學公式,在該公式適用的範圍(常數函式、一次函式、二次函式)中,平均變化率公式亦可寫成(和分別為函式在等於和處的導數),下證:
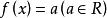 平均變化率
平均變化率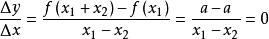 平均變化率
平均變化率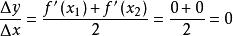 平均變化率
平均變化率①常數函式:對於一般的,先按原公式算,;按另一種方式算,,兩式結果相等,成立。
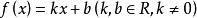 平均變化率
平均變化率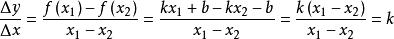 平均變化率
平均變化率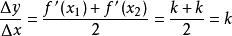 平均變化率
平均變化率②一次函式:對於一般的,先按原公式算,;按另一種方式算,,兩式結果相等,成立。
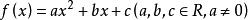 平均變化率
平均變化率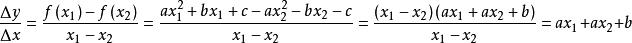 平均變化率
平均變化率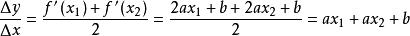 平均變化率
平均變化率③二次函式:對於一般的,先按原公式算,;按另一種方式算,,兩式結果相等,成立。
套用
觀察股票的變化速度
我們可以利用平均變化率的知識,求出一個股票在某一時間段的平均變化率,從而了解股票的趨勢以及未來的走勢。
為學習導數做鋪墊
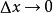 平均變化率
平均變化率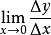 平均變化率
平均變化率導數是微積分裡面非常重要的一個知識點。導數可以理解為當時,平均變化率的極限,也就是。你看,導數其實就是平均變化率在增量趨向於0時的極限,我們先學習好平均變化率是不是可以更好的學習導數呢?