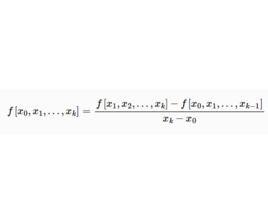定義
 差商
差商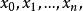 差商
差商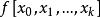 差商
差商 差商
差商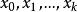 差商
差商給定函式和插值節點用表示關於節點的k階差商(k-th Difference Quotient)(k=1,2,…,n),它們可遞歸定義為
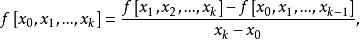 差商
差商 差商
差商 差商
差商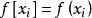 差商
差商其中關於節點的0階差商定義為其函式值,即。
差商表
 差商
差商可以構造差商表(表1),按列遞推計算的各階差商:
| 節點 | 0階差商 | 1階差商 | 2階差商 | 3階差商 | 4階差商 |  差商 差商 |
 差商 差商 | 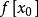 差商 差商 | |||||
 差商 差商 | 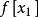 差商 差商 | 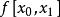 差商 差商 | ||||
 差商 差商 | 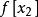 差商 差商 | 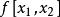 差商 差商 | 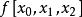 差商 差商 | |||
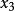 差商 差商 | 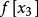 差商 差商 | 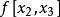 差商 差商 | 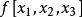 差商 差商 | 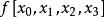 差商 差商 | ||
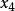 差商 差商 | 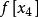 差商 差商 | 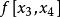 差商 差商 | 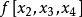 差商 差商 | 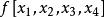 差商 差商 | 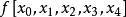 差商 差商 | |
 差商 差商 |  差商 差商 |  差商 差商 |  差商 差商 |  差商 差商 |  差商 差商 | 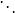 差商 差商 |
具體計算過程為
0階差商:
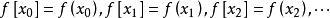 差商
差商1階差商:
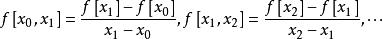 差商
差商2階差商:
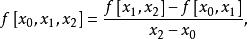 差商
差商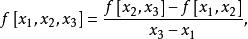 差商
差商 差商
差商3階差商:
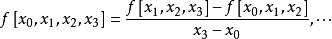 差商
差商 差商
差商差商的性質
根據差商的定義,利用數學歸納法可以證明差商具有如下性質:
性質1
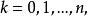 差商
差商對有
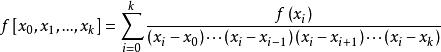 差商
差商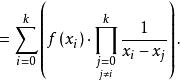 差商
差商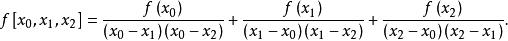 差商
差商如
性質2
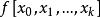 差商
差商(對稱性)差商與插值節點的順序無關,即
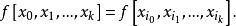 差商
差商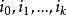 差商
差商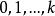 差商
差商其中是的任意一個排列。