路徑分析
正文
一種研究多個變數之間多層因果關係及其相關強度的方法。由美國遺傳學家S.賴特於1921年首創,後被引入社會學的研究中,並發展成為社會學的主要分析方法之一。路徑分析的主要目的是檢驗一個假想的因果模型的準確和可靠程度,測量變數間因果關係的強弱,回答下述問題:①模型中兩變數xj與xi間是否存在相關關係;②若存在相關關係,則進一步研究兩者間是否有因果關係;③若xj影響xi,那么xj是直接影響xi,還是通過中介變數間接影響或兩種情況都有;④直接影響與間接影響兩者大小如何。路徑分析的主要步驟是:①選擇變數和建立因果關係模型。這是路徑分析的前提。研究人員多用路徑圖形象地將變數的層次,變數間因果關係的路徑、類型、結構等,表述為所建立的因果模型。下圖是5個變數因果關係的路徑。
 路徑分析
路徑分析若變數間的關係是線性可加的,則圖中的因果模型可用3個標準化多元線性回歸方程表示:



 稱為殘差路徑係數,它表示所有自變數所不能解釋的因變數的變異部分,其大小對於因果模型的確定有重要作用。
稱為殘差路徑係數,它表示所有自變數所不能解釋的因變數的變異部分,其大小對於因果模型的確定有重要作用。 ②檢驗假設。路徑分析要以下列假定為前提:a.變數間的因果關係是單向的,不具有反饋性,又稱遞歸模型;b.變數間具有線性可加關係;c.變數具有等距以上測量尺度;d.所有誤差均為隨機的,外生變數無測量誤差;e.所有內生變數的誤差變數間及與內生變數有因果關係的所有自變數間無相關。當某些假定,如遞歸性或變數的測量尺度不滿足時,要做適當的處理才能套用路徑分析。
③估計參數。首先計算路徑係數與殘差路徑係數,然後計算兩變數間相關係數rji。此外,要計算兩變數間總因果作用力,包括變數xj對xi的直接作用力、xj經中間變數而對xi的間接作用力兩部分。例如,上圖的因果模型中,x1對x5的總作用力由直接作用力p51和間接作用力構成。這兩部分作用力的大小可由兩變數間的相關係數rij的分解得到。最後還要計算決定係數嵀,它表示所有作用於xi的自變數所能解釋xi變異量的比例。公式是:
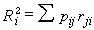
 ,一個理想的因果模型
,一個理想的因果模型 應當很小,當它很大時,則有必要重新估計此因果路徑,
應當很小,當它很大時,則有必要重新估計此因果路徑, 也可由公式
也可由公式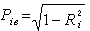 計算。c.進行F檢驗。
計算。c.進行F檢驗。 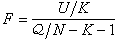
路徑分析是多元回歸分析的延伸,與後者不同的是:①路徑分析間的因果關係是多層次的,因果變數之間加入了中介變數,使路徑分析模型較一般回歸模型對於現實因果關係的描述更豐富有力。②路徑分析不是運用一個而是一組回歸方程,在分析時更應注意保證各方程式所含意義的一致性。
