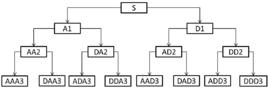
背景
傳統的振動信號分析和處理方法一般都是採用傅立葉分析,它是一個視窗函式固定不變的分析方法,無法反映信號的非平穩、持時短、時域和頻域局部化等特性 。
小波分析是一種視窗面積固定但其形狀可改變,即時間和頻率窗都可改變的時頻局部化分析方法,由於它在分解的過程中只對低頻信號再分解,對高頻信號不再實施分解,使得它的頻率解析度隨頻率升高而降低 。
在這種情況下,小波包分解應運而生。
小波包分析能夠為信號提供一種更加精細的分析方法。小波包分析將時頻平面劃分得更為細緻,它對信號的高頻部分的解析度比二進小波要高。而且,它在小波分析理論的基礎之上,引入了最優基選擇的概念。即,將頻帶經過多層次的劃分之後,根據被分析信號的特徵,自適應地選取最佳基函式,使之與信號相匹配,以提高信號的分析能力 。因此,小波包具有廣泛的套用價值。
從函式理論的角度來看,小波包變換是將信號投影到小波包基函式張成的空間中。從信號處理的角度來看,它是讓信號通過一系列中心頻率不同但頻寬相同的濾波器。
小波包
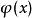 小波包分解
小波包分解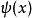 小波包分解
小波包分解設 和 分別是尺度函式和小波函式,令:
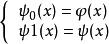 小波包分解
小波包分解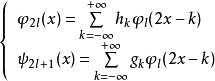 小波包分解
小波包分解 小波包分解
小波包分解 小波包分解
小波包分解則,定義的函式 稱為關於尺度函式 的 小波包
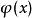 小波包分解
小波包分解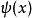 小波包分解
小波包分解設 和 分別是尺度函式和小波函式,令:
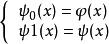 小波包分解
小波包分解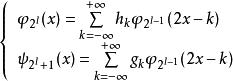 小波包分解
小波包分解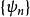 小波包分解
小波包分解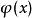 小波包分解
小波包分解則,定義的函式 稱為關於尺度函式 的 縮短小波包
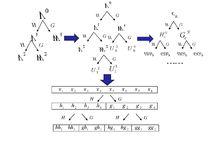
子空間分解過程
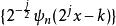 小波包分解
小波包分解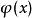 小波包分解
小波包分解函式族 稱為由尺度函式 生成的小波庫。
如下圖,為空間的小波包分解:
 小波包分解
小波包分解實際意義分析
參數j,k,n 的意義
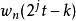 小波包分解
小波包分解小波庫中的一個函式:
 小波包分解
小波包分解參數 :尺度坐標
 小波包分解
小波包分解參數 :位置坐標
 小波包分解
小波包分解參數 :震盪次數
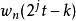 小波包分解
小波包分解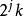 小波包分解
小波包分解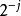 小波包分解
小波包分解 小波包分解
小波包分解是中心在 ,支集大小數量級為 ,震盪次數為 的小波函式
 小波包分解
小波包分解參數 固定
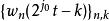 小波包分解
小波包分解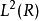 小波包分解
小波包分解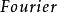 小波包分解
小波包分解小波庫中的函式 構成 的正交基,此時變換類似於一個加窗的 變換
 小波包分解
小波包分解參數 固定
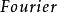 小波包分解
小波包分解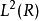 小波包分解
小波包分解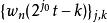 小波包分解
小波包分解小波庫中的函式 構成 的正交基,此時,變換是一個小波變換。
最優小波包基
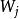 小波包分解
小波包分解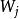 小波包分解
小波包分解在對函式或信號進行小波包分解時,由於 有不同的分解方式,即 有不同的正交基,因此,我們面臨“最優基”的選擇問題。
什麼是最優基?
如何選擇最優基?
代價函式
定義一個序列的代價函式,從小波庫的所有小波包基中尋找使代價函式最小的基 ,對一個給定向量來說,代價最小就是最有效的表示,此基便為“最優基”。
基本要求:
單調性
可加性(次可加性)
常用代價函式
 小波包分解
小波包分解 小波包分解
小波包分解①數列中大於給定門限的係數的個數。即預先給定一門限值 ,並計數數列中絕對值大於 的元素的個數
②範數:
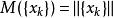 小波包分解
小波包分解通常選擇:
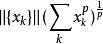 小波包分解
小波包分解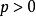 小波包分解
小波包分解其中, 範數越小,能量越集中
③熵:
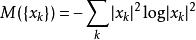 小波包分解
小波包分解④能量對數
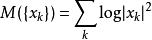 小波包分解
小波包分解