對邊簡介
常用在數學幾何題中,是數學中的專有名詞。這裡的“對”應取“對面的”的意思。
1)在三角形中,對邊為選定的一個角正對著的那條邊。例如:三角形△ABC,角A的對邊為邊BC。
2)在四邊形,特別是平行四邊形中,對邊為與選定的一條邊平行且相等的那條邊。
3)正四面體中,有6個邊。每個邊都和另外4條邊相交還剩下一個邊。這倆邊就是對邊。
直角三角形的對邊
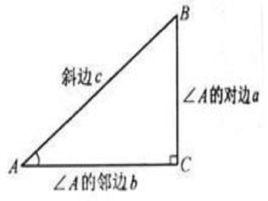
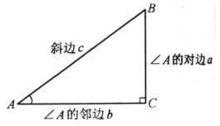 直角三角形示意
直角三角形示意三角形是由同一平面內不在同一直線上的三條線段‘首尾’順次連線所組成的封閉圖形,在數學、建築學有套用。
直角三角形是一個幾何圖形,是有一個角為直角的三角形,有普通的直角三角形和等腰直角三角形兩種。其符合勾股定理,具有一些特殊性質和判定方法。
如圖所示,AB是直角三角形的斜邊,對角A來說,BC是其對邊,AC是其鄰邊。
圓外切四邊形對邊性質
 圓外切四邊形
圓外切四邊形定理:圓外切四邊形對邊和相等。
證明:如圖,四邊形ABCD外切於圓O,E、F、G、H分別為AB、BC、CD、DA與圓O相切的切點,由圓的切線長定理得AE=AH,BE=BF , CF=CG , DG =DH,所以AE+BE+CG+DG=AH+BF+CF+DH,即AB+CD=BC+AD。
例題:如右圖,一圓內切於四邊形ABCD,且AB=16 , CD=10,則四邊形ABCD的周長為?
由定理可知,圓外切四邊形對邊和相等,所以AB+CD=BC+AD=26,所以四邊形周長為52。
對邊測量
隨著社會的進步和科學技術的發展,測繪新技術、新儀器在工程建設中得到了廣泛套用,集測距、測角及數據自動存儲、處理於一體的智慧型化測量儀器一全站儀,已相當普及。為了使全站儀在地形測量、地籍測量及施工放樣中發揮更大的作用,僅利用其測角和測距功能是遠遠不夠的,還需充分利用全站儀所提供的各種專項測量功能,如對邊測量等。
對邊測量是全站儀的一種專項測量功能,它可用來間接測量兩個不可通視點之間的水平距離。該方法設站靈活,操作簡單,但其測量精度沒有標註,需要通過計算求得。
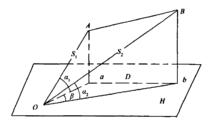 對邊測量示意圖
對邊測量示意圖對邊測量也稱為間接測距。當兩點之間不能商接測距時,可將全站儀安置在能夠觀測到兩點的任意位置,利用全站儀能同時觀測儀器與鏡站間的斜距、豎直角、水平角,間接計算兩鏡站點間的水平距離。如圖所示:A、B為地面上不能直接測距的兩點,在O點處安置全站儀,使儀器與A、B兩點能通視,起動全站儀對邊測量功能,分別照準A、B兩點的反光稜鏡,利用全站儀內置的對邊測量程式可直接顯示出A、B兩點間的水平距離D。