基本介紹
定義
 對稱雙線性型
對稱雙線性型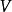 對稱雙線性型
對稱雙線性型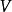 對稱雙線性型
對稱雙線性型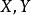 對稱雙線性型
對稱雙線性型定義1 設 是 上的雙線性型,若對 中任意向量 有
 對稱雙線性型
對稱雙線性型 對稱雙線性型
對稱雙線性型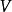 對稱雙線性型
對稱雙線性型則稱 是 上的 對稱雙線性型。
 對稱雙線性型
對稱雙線性型 對稱雙線性型
對稱雙線性型明顯地, 是對稱雙線性型的充要條件是, 的矩陣是對稱的。
 對稱雙線性型
對稱雙線性型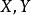 對稱雙線性型
對稱雙線性型定義2 設 是V上的雙線性型,若對V中任意向量 有
 對稱雙線性型
對稱雙線性型 對稱雙線性型
對稱雙線性型則稱 是V上的 反對稱雙線性型。
 對稱雙線性型
對稱雙線性型 對稱雙線性型
對稱雙線性型同樣有, 是反對稱雙線性型的充要條件是, 的矩陣是反對稱的。顯然,V上的一個任意的雙線性型都可以表示成對稱的和反對稱的雙線性型的和,而且,這種表示法是惟一的 。
相關定理
 對稱雙線性型
對稱雙線性型 對稱雙線性型
對稱雙線性型同一個雙線性型 對不同的基的矩陣是不同的,並且矩陣間具有契約關係,現在我們討論,在V中能否找到一組適當的基,使雙線性型 對這基的矩陣具有較簡便的形式,或者說,一個矩陣是否與對角形矩陣契約。(文中關於定理的證明請參考相應書籍)。
 對稱雙線性型
對稱雙線性型 對稱雙線性型
對稱雙線性型定理1 設 是數域K上n維線性空間V的對稱雙線性型,則V中存在一組基,使 對這基的矩陣是對角矩陣 。
顯然,定理1有下述兩種不同的提法:
(1)對稱矩陣必與對角形矩陣契約;
 對稱雙線性型
對稱雙線性型 對稱雙線性型
對稱雙線性型(2)對稱雙線性型 ,用適當的坐標變換 ,可化為標準形
 對稱雙線性型
對稱雙線性型這裡
 對稱雙線性型
對稱雙線性型實對稱雙線性型
以下討論實數域上線性空間V的對稱雙線性型(簡稱實對稱雙線性型)。
 對稱雙線性型
對稱雙線性型 對稱雙線性型
對稱雙線性型 對稱雙線性型
對稱雙線性型定理2 設 是實對稱雙線性型, ,則V中存在一組基,使 對這基的矩陣是
 對稱雙線性型
對稱雙線性型對應定理1之(2),這裡的標準形是
 對稱雙線性型
對稱雙線性型 對稱雙線性型
對稱雙線性型我們把這種形式的標準形稱為 的 規範形。
 對稱雙線性型
對稱雙線性型 對稱雙線性型
對稱雙線性型 對稱雙線性型
對稱雙線性型 對稱雙線性型
對稱雙線性型 對稱雙線性型
對稱雙線性型定理3 設 是實對稱雙線性型, ,則在 的對角形矩陣(3)中,“+1”的個數k是惟一的,因而“-1”的個數 也是惟一的,即 的規範形是惟一的。
 對稱雙線性型
對稱雙線性型 對稱雙線性型
對稱雙線性型 對稱雙線性型
對稱雙線性型 對稱雙線性型
對稱雙線性型 對稱雙線性型
對稱雙線性型在的規範形中,我們把正項個數k叫的 正慣性指數,負項個數叫的 負慣性指數,正慣性指數與負慣性指數的差叫的 符號差。
人所共知,實對稱矩陣可用正交矩陣化為實對角形矩陣,因此對於n維實內積空間中的對稱雙線性型,又可得
 對稱雙線性型
對稱雙線性型 對稱雙線性型
對稱雙線性型 對稱雙線性型
對稱雙線性型定理4 設是n維實內實積空間V的對稱雙線性型,,則V中必存在一組標準正交基,使對這組基的矩陣是
 對稱雙線性型
對稱雙線性型 對稱雙線性型
對稱雙線性型 對稱雙線性型
對稱雙線性型其中是的矩陣的不等於零的特徵根,而且它的對角陣是惟一的。此定理也常常被說成為實內積空間的對稱雙線性型可用正交變換化為標準形 。
復對稱雙線性型
最後討論複數域上線性空間V的對稱雙線性型(簡稱復對稱雙線性型),並且只討論特殊的復對稱雙線性型,即埃爾米特型。
 對稱雙線性型
對稱雙線性型 對稱雙線性型
對稱雙線性型定義 設V是複數域C上的有限維線性空間,若對任意,映射具有性質:
 對稱雙線性型
對稱雙線性型 對稱雙線性型
對稱雙線性型(1)即對於第一個變數是線性的;
 對稱雙線性型
對稱雙線性型 對稱雙線性型
對稱雙線性型(2)則稱是V上的一個埃爾米特型。
由(1)與(2),可推出:
 對稱雙線性型
對稱雙線性型 對稱雙線性型
對稱雙線性型 對稱雙線性型
對稱雙線性型即對於第二個變數是共軛線性的。
埃爾米特型與實對稱雙線性型具有相對應的性質,而且證明方法也類似,所以在下面只把結果列出。
 對稱雙線性型
對稱雙線性型 對稱雙線性型
對稱雙線性型 對稱雙線性型
對稱雙線性型 對稱雙線性型
對稱雙線性型 對稱雙線性型
對稱雙線性型 對稱雙線性型
對稱雙線性型 對稱雙線性型
對稱雙線性型 對稱雙線性型
對稱雙線性型設是V上的一個埃爾米特型,它對基的短陣是A,到的過渡矩陣是P,則或是對的矩陣。
 對稱雙線性型
對稱雙線性型 對稱雙線性型
對稱雙線性型設A,B均為n階矩陣,若存在可逆矩陣Q,使,則稱A與B是埃爾米特契約的;由此可以說,同一個埃爾米特型對不同基的矩陣是埃爾米特契約的。矩陣間的埃爾米特契約具有自反性,對稱性和傳遞性,而且埃爾米特型的矩陣的秩與基的選擇無關。
 對稱雙線性型
對稱雙線性型 對稱雙線性型
對稱雙線性型設是埃爾米特型,,則有
 對稱雙線性型
對稱雙線性型 對稱雙線性型
對稱雙線性型 對稱雙線性型
對稱雙線性型(1)V中必存在一組基,使對這組基的矩陣是對角矩陣,其中“+1”的個數是是惟一的,因而“一1”的個數也是惟一的;
 對稱雙線性型
對稱雙線性型 對稱雙線性型
對稱雙線性型 對稱雙線性型
對稱雙線性型 對稱雙線性型
對稱雙線性型(2)V中必存在一組標準正交基,使對這組基的矩陣是對角矩陣,其中是的矩陣的不等於零的特徵根,而且這對角陣是惟一的 。

