將軍飲馬問題

將軍飲（yìn）馬的科學計算依據：首先，我們給大家介紹一下對稱點的概念。已知一條直線L和直線外一點A，求A點關於L的對稱點A`我們用的方法是A點向L引垂線，垂足為O，延長AO至A`，使OA'=OA，則A`點即為所求。 A 其次，我們介紹一下"將軍飲馬"問題。據說，在古希臘有一位聰明過人的學者，名叫海倫。有一天，一位將軍向他請教了一個問題：從A地出發到河邊飲馬，然後再B地，走什麼樣的路線最短？如何確定飲馬的地點？提起路線最短的問題，大家知道：連結兩點之間所有線中，最短的是線段。這個題中馬走的是一條折線。這又該怎么辦呢？海倫的方法是這樣的：設L為河。作AO L交L於O點，延長AO至AKL，使ALLO=AO，連結AKLB交L於C點，則C 點即為所求的點。連結AC。（AC+CB）為最短路程。這是因為，ALK點是A點關於L 的對稱點，顯然，AC=ADFC。因為ASDBSHI是一條線段，所以AC+CB==AASC+CB=AKDBYEYE也就是最短。少年朋友們喜歡打檯球吧，實際上打檯球無時無刻都需要套用海倫的妙法。下面我們看一個有關打檯球的實例。若在矩形的球檯上，有兩個球在M和N的位置上。假如從M打出球，先觸及DC邊K點，彈出後又觸到CB邊E點，從CB邊再反射出來。問用怎樣的打法，才能使這個球反射後正好撞上在N 點放置的球？具體做法是： 先作M關於DC的對稱點MLJLK，再作LKJ；L關於BC 的對稱點LKJ那么MKJN和BC 的交點為E，DKL；S和CD 交於K，E、K就是球和各邊的撞擊點。按MK遮掩的踐線打球，一定會使球M從BC邊彈出後撞上球N。

基本信息

• 中文名：將軍飲馬問題
• 英文名：The general problem of Yin

• 出處：唐朝詩人李欣的詩《古從軍行》
• 最早出現：古羅馬時代

問題概述

唐朝詩人李頎的詩《古從軍行》開頭兩句說：“白日登山望烽火，黃昏飲馬傍交河． ”詩中隱含著一個有趣的數學問題．

將軍飲馬問題

如圖所示，詩中將軍在觀望烽火之後從山腳下的A點出發，走到河邊飲馬後再到B點宿營．請問怎樣走才能使總的路程最短？

這個問題早在古羅馬時代就有了，傳說亞歷山大城有一位精通數學和物理的學者，名叫 海倫．一天，一位羅馬將軍專程去拜訪他，向他請教一個百思不得其解的問題．

將軍每天從軍營A出發，先到河邊飲馬，然後再去河岸同側的B地開會，應該怎樣走才能使路程最短？

從此，這個被稱為“ 將軍飲馬”的問題廣泛流傳．

這個問題的解決並不難，據說海倫略加思索就解決了它．

解決辦法

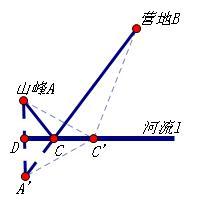將軍飲馬問題

如圖所示，從A出發向河岸引垂線，垂足為D，在AD的延長線上，取A關於河岸的對稱點A'，連結A'B，與河岸線相交於C，則C點就是飲馬的地方，將軍只要從A出發，沿直線走到C，飲馬之後，再由C沿直線走到B，所走的路程就是最短的．

如果將軍在河邊的另外任一點C'飲馬，所走的路程就是AC'+C'B，但是，AC'+C'B=A'C'+C'B>A'B=A'C+CB=AC+CB．

可見，在C點外任何一點C'飲馬，所走的路程都要遠一些．

這有幾點需要說明的：（1）由作法可知，河流l相當於線段AA'的中垂線，所以AD=A'D。（2）由上一條知：將軍走的路程就是AC+BC，就等於A'C+BC，而兩點確定一線，所以C點為最優。

套用拓展

將軍飲馬問題

如圖，有A、B兩個村莊，他們想在河流l的邊上建立一個水泵站，已知每米的管道費用是100元，A到河流的距離AD是1km，B到河流的距離BE是3km，DE長3km。請問這個水泵站應該建立在哪裡使得費用最少，為多少？

解：如圖所作，C點為水泵站的位置。

依題意，得：所鋪設的水管長度就是AC+BC，即：A'C+BC=A'B的長度。

因為EF=A'D=AD=1km, 所以BF=BE+EF=4km

又A'F=DE=3km

在Rt△A'BF中，A'B^2=A'F^2+BF^2

所以：解得：A'B=5km

所以總費用為：5*1000*100=500000（元）