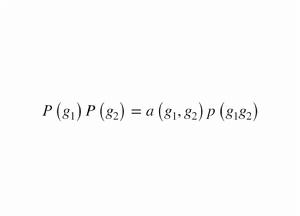定義
設G為一個群,K為域,n為正整數。把K上n維線性空間V的全線性群記作GL(V)。G 到GL(V)的映射P稱為G 的具有因子集a的射影表示,如果對所有的g₁,g₂,∈ G,均有
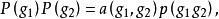 射影表示
射影表示這裡 a 為積集合G × G到乘法群Kˣ的映射。G的射影表示P稱為不可約的,如果V中沒有非平凡子空間W,使W在一切P(g),g ∈ G下不變。
設GL(V₁),GL(V₂) 分別是K上線性空間V₁,V₂的全線性群。P₁和P₂分別是G到GL(V₁)內的,和到GL(V₂) 內的射影表示。說P₁,P₂是等價的,如果有V₁到V₂的同構映射T使對一切 g ∈ G,
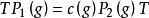 射影表示
射影表示成立,這裡c為G到Kˣ的映射。
當K為特徵0的代數封閉域時,有限群G的不可約射影表示的次數為G的階的因子。
表示論
為了了解一個群的構造,我們常常研究它到某個具體的群內的同態。我們將這種同態稱為表示。最常見的具體的群有矩陣群(即矩陣組成的群)和置換群,所以常見的表示就是矩陣表示和置換表示。在矩陣表示的情況下,人們自然地把矩陣當成線性變換來看待,從而可以使用線性代數的豐富成果以得到深入的結論。