基本介紹
距離的射影測度(射影距離)和夾角的射影測度(射影角度)合稱為射影測度(projective measure)。射影測度是凱萊(A.Cayley)於1859年建立的,1871年,克萊因(C.F.Klein)利用射影測度的概念來說明非歐幾何學。非退化的二階曲線有實虛兩種情況,若絕對形為非退化的實二階曲線,則可構成羅氏幾何;若絕對形為非退化的虛二階曲線,則可構成黎氏幾何,這兩種幾何合稱非歐幾何,這樣非歐幾何就可以從射影測度的概念導出,因為射影測度是由交比來定義的,它屬於射影性質,所以非歐幾何可以利用射影測度從射影幾何導出 。
 射影角度
射影角度 射影角度
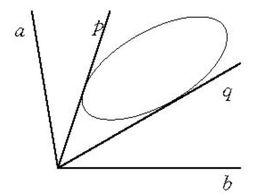
射影角度在平面內,取定一條常態二級曲線,並選定一常數k(k≠0)。對於平面內的任意兩條直線a、b,從它們的交點引的兩條切線t、t(圖1),作函式
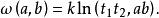 射影角度
射影角度因為二直線a、b確定以後,它們的交點也就唯一地確定,二切線t、t隨即也被確定,由於
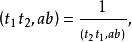 射影角度
射影角度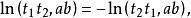 射影角度
射影角度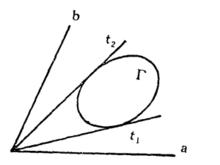 圖1
圖1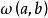 射影角度
射影角度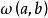 射影角度
射影角度所以函式由二直線a、b唯一確定(除符號外)。利用交比的性質,可以驗證函式滿足下列三個條件 :
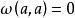 射影角度
射影角度1.,
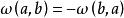 射影角度
射影角度2.;
3.若直線a、b、c相交於一點,則
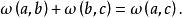 射影角度
射影角度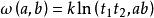 射影角度
射影角度 射影角度
射影角度定義函式稱為二直線a、b的有向夾角的射影測度,簡稱為射影角度。預先規定的二級曲線稱為這測度的絕對形,常數k稱為測度係數 。
下面我們研究射影角度的表達式。
 射影角度
射影角度設二級曲線(給定的絕對形)的方程為
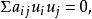 射影角度
射影角度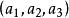 射影角度
射影角度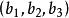 射影角度
射影角度二直線a、b的坐標分別為及,由a、b的交點所引的二切線t、t(它們a、b屬於同一線束)的坐標可以表為
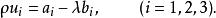 射影角度
射影角度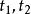 射影角度
射影角度 射影角度
射影角度由於與二級曲線相切,故有
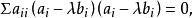 射影角度
射影角度展開,得
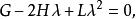 射影角度
射影角度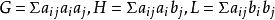 射影角度
射影角度其中。
所以
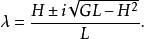 射影角度
射影角度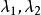 射影角度
射影角度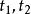 射影角度
射影角度如果以表示這兩個根,那么的坐標分別為
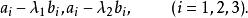 射影角度
射影角度因此
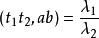 射影角度
射影角度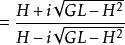 射影角度
射影角度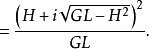 射影角度
射影角度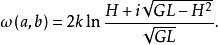 射影角度
射影角度關於射影角度,我們有如下的定理。
定理如果二直線的交點在絕對形上,則它們的夾角的射影測度等於零。
 射影角度
射影角度 射影角度
射影角度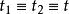 射影角度
射影角度證明若二直線a、b的交點在絕對形上,過此交點所引的的兩條切線重合為一條直線,即,交比(tt,ab)=1。
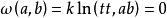 射影角度
射影角度。
定理說明,兩條平行直線所成的夾角等於零 。
相關概念
 射影角度
射影角度 射影角度
射影角度在平面內,給定一條常態的二階曲級 ,並選定一常數K(K≠0)。對於平面內的任意兩點A、B,它們的連線交二階曲線 於P、P(圖2),作函式
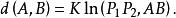 射影角度
射影角度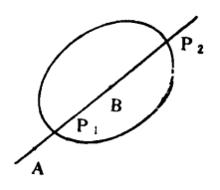 圖2
圖2函式d(A,B)被A、B兩點唯一確定(除符號外),利用交比的性質,可以驗證函式d(A,B)滿足下列三個條件;
1.d(A,A)=0;
2.d(A,B)=-d(B,A);
3.若A、B、C是一直線上的三點,則d(A,B)+d(B,C)=d(A,C)。
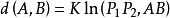 射影角度
射影角度 射影角度
射影角度定義函式 稱為兩點A、B間的有向距離的射影測度,簡稱為 射影距離。預先規定的二階曲線稱為這測度的絕對形,常數K稱為測度係數 。
 射影角度
射影角度設二階曲線的方程為
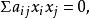 射影角度
射影角度二點A,B的坐標分別為(a,a,a)及(b,b,b),類似地可求出射影距離的表達式
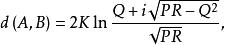 射影角度
射影角度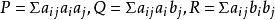 射影角度
射影角度其中 。
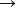 射影角度
射影角度 射影角度
射影角度 射影角度
射影角度由射影距離的定義還可以看出,當A(或B) P(或P)時,交比(PP,AB) 0,d(A,B) 。因此有
定理平面上任何一點與絕對形上的任何點間的射影距離為無窮大。
 射影角度
射影角度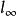 射影角度
射影角度由定理可以看出,作為絕對形的二階曲線 與歐氏測度中的無限遠直線 相當。
定義設二直線的交點在實的絕對形上,則稱這二直線為平行直線 。